Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 23

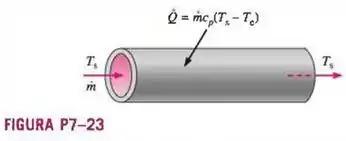
A água fria entra em um tubo, onde ela é aquecida por uma fonte de calor externa (Figura P7-23). As temperaturas de entrada e saída da água são , respectivamente. A taxa total de transferência de calor da vizinhança para a água do tubo é

onde é a taxa de escoamento de massa através do tubo e é o calor específico da água. Escreva as dimensões primárias de cada termo aditivo da equação e certifique-se de que a equação é dimensionalmente homogênea. Mostre todo o seu trabalho.

Passo 1

Oi pessoal, tudo bem?

Devemos primeiramente lembrar que as principais dimensões da taxa de transferência de calor são . As principais dimensões da vazão mássica são e calor específico são .

Em resumo, somente relembramos as dimensões primárias de cada termo. Vamos agora ver se a equação é dimensionalmente homogênea.

Passo 2

Bem, relembrando, a equação é:

Assim, cada termo na equação pode ser escrito em termos de dimensões primárias:

Primeiro, a taxa de transferência de calor:

Obs: Lembrando que (segunda Lei de Newton)

Continuando a dedução, encontramos:

Passo 3

Agora:

Continuando a dedução, encontramos:

Obs: Lembrando que:

Resposta

Portanto, foi provado que a equação é dimensionalmente homogênea.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um escoamento em regime não permanente e unidimensional em uma fina camada de líquido é descrito pela equação ∂ u ∂ t + u ∂ u ∂ x = - g ∂ h ∂ x Use uma escala de comprimento, L , e uma escala de veloc

Um escoamento em regime transiente, bidimensional, compressível e não viscoso pode ser descrito pela equação ∂ 2 ψ ∂ t 2 + ∂ u 2 + v 2 ∂ t + u 2 - c 2 ∂ 2 ψ ∂ x 2 + v 2 - c 2 ∂ 2 ψ ∂ y 2 + 2 u v ∂ 2 ψ

Usando análise de ordem de grandeza, as equações da continuidade e de Navier Stokes podem ser simplificadas para as equações de camada limite de Prandtl. Para escoamento em regime permanente, incomp

A equação descrevendo o movimento de um fluido em um tubo, quando o escoamento parte do repouso devido a um gradiente de pressão aplicado, é ∂ u ∂ t = - 1 ρ ∂ p ∂ x + v ∂ 2 u ∂ r 2 + 1 r ∂ u ∂ r Use a

Explique a l e id ah o m o g e n e i d a d ed i m e n s i o n a l em termos simples.