Um termógrafo de infravermelho (IV) é um radiômetro que fornece uma imagem de um cenário alvo, indicando a temperatura aparente dos elementos no cenário em termos de uma escala de brilho branco e preto ou colorida azul e vermelho. A radiação originada de um elemento no cenário alvo incide sobre o detector de radiação, que fornece um sinal proporcional à taxa de energia radiante incidente. O sinal estabelece a escala de brilho ou de cor para o ponto da imagem (pixel) associado ao elemento. É proposto um procedimento para a calibragem do campo de um termógrafo de infravermelho que tem um detector de radiação cuja banda de passagem espectral está localizada entre e . Uma placa metálica aquecida, que é mantida a e tem quatro revestimentos difusos e cinzas com emissividades diferentes, é focalizada pelo termógrafo IV em local com uma vizinhança a .

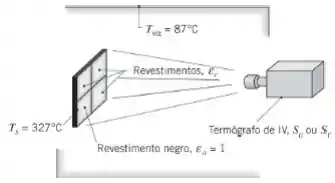
(a) Considere o sinal de saída do termógrafo quando ele está examinando o revestimento negro, . A radiação que atinge o detector é proporcional ao produto entre o poder emissivo de corpo negro (ou intensidade emitida) na temperatura da superfície e a fração da banda de emissão corresponde à banda de passagem espectral do termógrafo IV. A constante de proporcionalidade é conhecida por responsividade, Escreva uma expressão para o sinal de saída do termógrafo, , em termos de , do poder emissivo de corpo negro do revestimento e da fração apropriada da banda de emissão. Supondo , avalie

(b) Considere o sinal de saída do termógrafo quando ele está examinando um dos revestimentos com emissividade menor do que a unidade. A radiação vinda do revestimento atinge o detector devido à emissão e à reflexão da irradiação da vizinhança. Escreva uma expressão para o sinal, , em termos de , do poder emissivo de corpo negro do revestimento, do poder emissivo de corpo negro da vizinhança, da emissividade do revestimento e das frações apropriadas de banda de emissão. Para os revestimentos cinzas e difusos, a refletividade é .

(c) Supondo , avalie os sinais de saída do termógrafo, quando ele estiver apontado para painéis com emissividades de e

(d) O termógrafo é calibrado de forma que o sinal (do revestimento negro) irá fornecer uma indicação de escala correta para. Os sinais dos outros três revestimentos, , são menores do que . Desse modo, o termógrafo irá indicar uma temperatura aparente (de corpo negro) inferior a . Estime as temperaturas indicadas pelo termógrafo para os três painéis da parte (c).

Para resolver essa questão vamos assumir que:

(1) A placa possui temperatura uniforme;

(2) Os arredores são isotérmicos e grandes em comparação com a placa;

(3) Os revestimentos são difusos e cinza, de modo que e .

Ao visualizar o revestimento preto o sinal de saída do scanner pode ser expresso como:

Onde é a responsividade ) é a potência emissiva do corpo negro em e é a fração da banda espectral entre e no espectro para uma corpo negro em ,

Onde as frações são avaliados usando a Tabela 12.1 com,

E,

Substituindo valores numéricos por , encontramos,

Ao visualizar um dos revestimentos o sinal de saída será afetado pela emissão e irradiação refletida do ambiente,

Onde os parâmetros de irradiação refletida são,

E as frações de banda relacionadas são,

Combinando as equações acima, o sinal de saída do scanner ao visualizar um revestimento é,

Substituindo os valores numéricos na equação acima, encontramos:

Onde parae

Para , temos que: