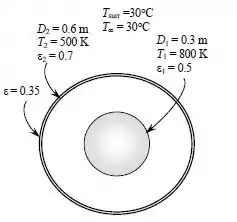
Duas esferas concêntricas de diâmetro D1 = 0,3 m e D2 = 0,6 m são mantidas a temperaturas uniformes de T1=800K e T2=500K e tem emissividades 0,5 e 0,7, respectivamente. Determine a taxa líquida de transferência de calor por radiação entre as duas esferas. Além disso, determine o coeficiente de transferência de calor por convecção na superfície externa, considerando que tanto o meio quanto as superfícies circundantes estão em torno de 30°C. Considere que a emissivdade da superfície externa é 0,35.

Para calcularmos o coeficiente convectivo, precisamos fazer um balanço de energia na superfície externa!

Discussão: esse coeficiente baixo faz muito sentido uma vez que estamos numa condição de escoamento natural, ou seja, baixíssimas velocidades, onde as correntes de convecção são formadas pelas diferenças de temperatura!