Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 36

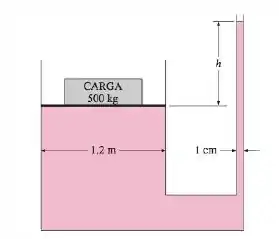
A carga de 500 kg do macaco hidráulico mostrado na figura abaixo deve ser elevada despejando-se óleo ( ρ = 780   k g / m ³ ) dentro de um tubo fino. Determine quão alto h deve ser para começar a levantar o peso.

Passo 1

Essa questão é um pouco física 1 rsrsrs mas também você vai ver que é bem suave de ser resolvida.

Primeira coisa que vamos determinar é a pressão que essa carga faz sobre a superfície em que ela se encontra, ok?

P c a r g a = F p e s o A = m g π D 2 4 = 500 k g 9,81 m / s ² π 1,2 m 2 4 1 k N 1000   k g . m s 2 = 4,34 k N m 2 = 4,34   k P a

MAS DE ONDE SURGIU AQUELE FATOR ALI, CARA?

Vamos lá que te explico! Esse é um fator de conversão muito importante e vamos usar demais durante as resoluções de exercícios.

Fazendo uma análise dimensional rápida a gente vai ver que essa pressão não vai sair em Pa, se liga!

m g π D 2 4 = k g   x   m s 2 m 2 = k g m . s

Olha que zoado a unidade!!!

Então, a gente quer que esse bendito se transforme em kPa que nada mais é do que Pressão = F/A = N/m², certo?

Então no final das contas a gente pode mexer nas unidades pra aparecer o nosso N/m².

Se a gente pegar F = m . a = k g m s 2 = N , certo?

Agora vamos pegar a pressão, a gente escreve que P = N m 2

Ou seja, 1Pa = 1 N/m². Olha que maravilha como essas duas unidades lá de força e pressão podem se relacionar bem:

1 N 1 k g . m s 2 1 k P a 1000 N m 2 = 0,001 k P a k g m . s  

Ou ainda podemos dizer o seguinte:

1   k P a = 1 k N m 2 = 1000   k g m s 2

Essa relação é MUITO IMPORTANTE!!!

Passo 2

A gente também sabe que vamos precisar então que uma pressão de coluna de óleo seja feita tal que tenha no mínimo o mesmo valor da pressão da carga, logo...

P c a r g a = ρ g h → h = P c a r g a ρ g = 4,34 k N m 2 780 k g m 3 9,81 m s 2 1000   k g . m 2 s 1 k N / m ² = 0,57   m

Resposta

Precisamos de uma coluna de óleo com 0,57m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um certo processo industrial, óleo de massa específica ρ escoa através do tubo inclinado da Figura PA3.1. Um manômetro tipo-U, com fluido de massa específica ρ m , mede a diferença de pressão entre
Water flows downward in a pipe at 458, as shown inFig. P2.44. The pressure drop p1 2 p2 is partly due to gravityand partly due to friction. The mercury manometer reads a6-in height difference. What is
For the traditional equal-level manometer measurement inFig. E2.3, water at 208C flows through the plug devicefrom a to b. The manometer fl uid is mercury. If L 5 12 cmand h 5 24 cm, (a) what is the p
For gases that undergo large changes in height, the linearapproximation, Eq. (2.14), is inaccurate. Expand the troposphere power-law, Eq. (2.20), into a power series, andshow that the linear approxima
If the absolute pressure at the interface between water andmercury in Fig. P2.16 is 93 kPa, what, in lbf/ft2, is (a) thepressure at the surface and (b) the pressure at the bottom ofthe container?