Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 125

A uniform cylindrical white oak log, ρ = 710 kg/m3, floats

lengthwise in fresh water at 208C. Its diameter is 24 inches.

What height of the log is visible above the surface?

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Desenhando o diagrama do deslocamento da água

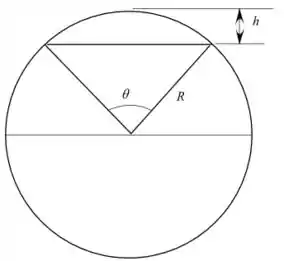
Passo 2

Escreva a relação para calcular a altura do log é visível acima da superfície.

h R = 1 - c o s ⁡ θ 2 . . . ( 1 )

Aqui, h é a altura do tronco é visível acima da superfície, e é R o raio do carvalho cilíndrico. Escreva a relação para calcular as proporções de áreas do segmento e do círculo.

A s A e = 1 - ρ s ρ c . . . ( 2 )

Aqui, A s é a área do segmento, A c é a área do círculo, ρ s é a densidade do carvalho branco, e ρ c é a densidade da água.

Passo 3

Calcule a área do segmento.

A s = R 2 2 π × θ 180 - s i n ⁡ θ

Calcule a área do círculo.

A c = π R 2

Obtenha os valores de "Propriedades da água da Tabela A.1". À temperatura 20 ∘ C .

ρ = 998   k g / m 3

Substituindo valores na equação (2)

A s A c = 1 - ρ s ρ c R 2 2 π × θ 180 - s i n ⁡ θ π R 2 = 1 - 710   k g / m 3 998   k g / m 3 1 2 θ 180 - s i n ⁡ θ = 0.289

Passo 4

Iterar o valor de θ .

θ = 140.5 ∘

Substituindo valores

h R = 1 - c o s ⁡ θ 2 h 12 i n . = 1 - c o s ⁡ 140.5 ∘ 2 h = 12 i n . ( 1 - 0.338 )   = 7.94 i n .

Assim, a altura do tronco é visível acima da superfície é 7.94 i n .

Resposta

h = 7.94 i n

Exercícios de Livros Relacionados

Considere que o balão do Problema P2.111 seja construído para ter um diâmetro de 14m , cheio ao nível do mar com ar quente a 70 ℃ ℃ e 1a t m , e seja liberado. Se o ar dentro do balão permanecer const
Uma barcaça tem 4,5m de largura e 12m de comprimento e flutua com um calado de 1,2m . Ela recebe uma carga de cascalho tal que seu centro de gravidade está 0,6m acima da linha d’água. Ela é estável?
Um bloco de madeira ( d =0,6 ) flutua em um fluido X , como na Figura P2.126, de forma que 75 % de seu volume está submerso nesse fluido. Calcule a pressão vacuométrica do ar no tanque.
Um cone circular reto sólido tem d = 0,99 e flutua verticalmente como na Figura P2.132. Essa é uma posição estável para o cone?
Considere um cilindro de densidade d1 flutuando verticalmente na água ( d = 1 ) , como na Figura P2.127. Deduza uma fórmula para os valores estáveis de D / L em função de d e aplique-a ao caso D / L =