Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 16

The centrifugal pump in Fig. P11.16 has r1 5 15 cm,

r2 5 25 cm, b1 5 b2 5 6 cm, and rotates counterclockwise

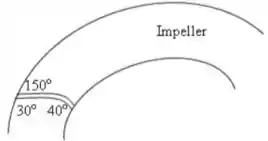
at 600 r/min. A sample blade is shown. Assume α1 5 908.

Estimate the theoretical fl ow rate and head produced, for

water at 208C, and comment.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

O diagrama mostra uma lâmina de uma bomba centrífuga rotacionando no sentido anti-horário

Passo 2

Calcular a velocidade angular utilizando a equação,

ω = 2 π N 60

Aqui a velocidade de ração da lâmina é N Substituta 600 r / m i n para N Consequentemente,

ω   = 2 π × 600 60   = 62.83 r a d / s

Calcular a velocidade circunferencial,

u 1 = ω r 1

Aqui a velocidade angular é ω e o raio interno da lâmina é r 1

Agora substituindo 62.8 r a d / s para ω e 0.15   m para r 1

u 1   = 62.8 × 0.15   = 9.425   m / s

Encontre também a velocidade na periferia externa,

u 2 = ω r 2

Aqui, o raio externo da lâmina é r 2 Agora substituindo 62.8 r a d / s para ω e 0.25   m para r 2

u 2   = 62.8 × 0.25   = 15.7   m / s

Passo 3

Do diagrama, uma vez que a rotação é anti-horária, β 2 = 150 ∘ e também é dado α 1 = 90 ∘ de modo que a velocidade tangencial,

V t 1 = 0

Calcular a velocidade normal por,

V n 1 = u 1 t a n ⁡ β 1

Aqui, o ângulo da lâmina na entrada é β 1 Substituindo 9.425 para u 1 e 40 ∘ para β 1

V n 1   = 9.425 × t a n ⁡ 40 ∘   = 7.91   m / s

Agora calcular a taxa de fluxo é dado por,

Q = 2 π r 1 b 1 V n l

Aqui, a largura da lâmina na entrada é b 1 Substituindo 0.15   m para r 1 , 6   c m = 0.06   m b 1 e 7.91   m / s para V n 1

Q   = 2 π × 0.15 × 0.06 × 7.91   = 0.44729   m 3 / s   = 0.448 × 15850.32   = 7100.94 g a l / m i n

Portanto, a taxa de fluxo teórica Q é 7100.94 g a l / m i n .

Passo 4

A cabeça teórica é,

H = u 2 2 g - u 2 V n 2 c o t ⁡ β 2 g

Aqui a velocidade normal na saída é V n 2 e o ângulo da lâmina na saída é β 2 Da equação da continuidade,

V n 2 = Q A 2

Aqui a área de superfície da bomba na saída é, A 2 portanto,

H = u 2 2 g - u 2 c o t ⁡ β 2 2 π r 2 b 2 g Q

Agora substitua 15.7   m / s por u 2 , 9.81   m / s 2 para g , 0.25   m para r 2 , 6   c m = 0.06   m para b 2 , 0.448   m 3 / s para Q e 150 ∘ para β 2

H   = 15.7 2 9.81 - 15.7 c o t ⁡ 150 ∘ 2 π × 0.25 × 0.06 × 9.81 0.447   = 38.27   m

Portanto, a cabeça teórica é H = 38.27   m .

Resposta

Q = 7100.94 g a l / m i n

H = 38.27   m

Exercícios de Livros Relacionados

14-9 Um compressor de ar aumenta a pressão e a densidade ( P sP c ) do ar que passa através dele (Figura P14-9). No caso em que os diâmetros de saída e entrada são iguais ( D s = D e ) , como a veloci
14-13C Defina carga de sucção líquida positiva e carga de sucção líquida necessária positiva, e explique como essas duas quantidades são usadas para garantir que não haja cavitação emuma bomba.
14-12C A Figura P14-12C mostra dois locais possíveis para uma bomba d"água em um sistema de tubulação que bombeia água do tanque mais baixo para o tanque mais alto. Qual local émelhor? Por quê?
14-14C Considere o escoamento através de uma bomba de água. Para cada declaração, selecione se ela é verdadeira ou falsa e discuta rapidamente sua resposta.(a) Quanto mais rápido for o escoamento atra
14-8 Uma bomba d'água aumenta a pressão da água que passa através dela (Figura P14-8). Estima-se que a água seja incompressível. Para cada um dos três casos listados abaixo, como avelocidade média da