Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 14

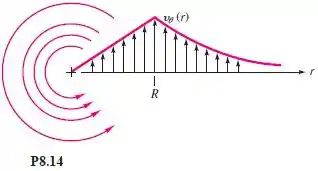
Um tornado pode ser modelado como o escoamento circulatório mostrado na Figura P 8.14 , com v r = v z = 0 e v θ ( r ) dado por

v θ = ω r                         r ≤ R ω R 2 r                 r > R

Determine se esse padrão de escoamento é irrotacional na região interna e na externa. Usando a equação da quantidade de movimento em r   D . 5 do Apêndice D , determine a distribuição de pressões p ( r ) no tornado, considerando p = p ∞ quando r   → ∞ . Encontre o local e a intensidade da pressão mais baixa.

Passo 1

E aí, tudo bem? Bora matar essa questão rapidinho!

Primeiro vamos avaliar o escoamento para as regiões externa e interna.

Região interna:

Ω z = 1 r d d r r v θ = 1 r d d r r ω r

Ω z = 2 ω

Região externa:

Ω z = 1 r d d r r v θ = 1 r d d r r ω R 2 r

Ω z = 0

Logo a região interna se trata da rotação de um corpo sólido e a parte interna é irrotacional!

Passo 2

Podemos calcular a pressão integrando o momento em relação ao raio usando a equação D - 5 no apêndice:

Para a região externa:

d p d r = ρ ⋅ v θ 2 r

p e x t = ∫ ρ r ω R 2 r 2 d r = ∫ ρ ω 2 R 4 r 3 d r

p e x t = - ρ ω 2 R 4 r 2 + C

Em r = ∞ , p = p ∞ .

p e x t = p ∞ - ρ ω 2 R 4 2 r 2

Fazendo a mesma coisa para a região interna:

p i n t = ∫ ρ r ω r 2 d r = ρ ω 2 r 2 2 + C

Como em r = R :

p R = p ∞ - ρ ω 2 R 2 2

Finalmente temos:

p i n t = p ∞ - ρ ω 2 R 2 + ρ ω 2 r 2 2

Passo 3

Pra matar de vez nossa questão só precisamos avaliar as equações, vamos montar um gráfico organizando nossas equações:

Podemos ver que a pressão mínima ocorre na origem onde r = 0 e a pressão é dada por:

p m í n = p ∞ - ρ ω 2 R 2

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

A região interna se trata da rotação de um corpo sólido e a parte interna é irrotacional!

p e x t = p ∞ - ρ ω 2 R 4 2 r 2

p i n t = p ∞ - ρ ω 2 R 2 + ρ ω 2 r 2 2

p m í n = p ∞ - ρ ω 2 R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Fontes bidimensionais de mesma intensidade m = Ua, sendo U uma velocidade de referência, são localizadas em (x, y)= (0, a) e (0, –a). Trace as linhas de corrente e as equipotenciais no semiplano super
Considere o escoamento fonte/vórtice da Equação (8.16) simulando um tornado, como na Figura 8.25. Admita que a circulação em torno do tornado seja Γ =8.500m ² / s ² e que a pressão em r = 40 m seja 2.
Uma corrente de água uniforme U ∞ =20m / s e ρ =998k g / m ³ ³ é combinada com uma fonte na origem para formar um semicorpo. Em (x, y) = (0, 1,2 m), a pressão é 12,5 kPa abaixo de p ∞ . (a) Esse ponto
Um semicorpo de Rankine é formado como mostra a Figura P8.31. Para a velocidade da corrente e as dimensões do corpo mostradas, calcule (a) a intensidade da fonte m em m²/s, (b) a distância a, (c) a di
Trace as linhas de corrente, especialmente o formato do corpo, causadas por fontes de igual intensidade + m em (-a, 0) e (+a, 0) mais uma corrente uniforme U ∞ =m a .