Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 25

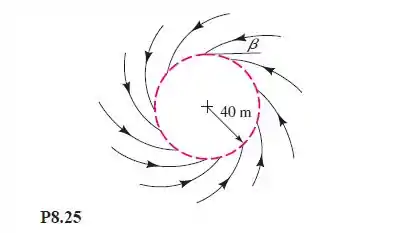
Considere o escoamento fonte/vórtice da Equação (8.16) simulando um tornado, como na Figura 8.25. Admita que a circulação em torno do tornado seja Γ =   8.500   m ² / s e que a pressão em r = 40 m seja 2.200 Pa abaixo da pressão do campo não perturbado (distante). Considerando escoamento não viscoso com massa específica ao nível do mar, avalie: (a) a intensidade adequada da fonte - m, (b) a pressão em r = 15 m e (c) o ângulo β com o qual as linhas de corrente atravessam o círculo em r = 40 m (ver a Figura P8.25).

Passo 1

Bora pra mais uma!

A circulação produz a velocidade circunferencial em r=40m:

v θ = Γ 2 π r = 8500 2 π 40 = 33,8 m s

Assumimos que a massa específica a nível do mar é ρ = 1225 k g / m 3 , e então podemos usar Bernoulli para achar a velocidade radial:

P ∞ + ρ 2 0 2 = P ∞ - ∆ P + ρ 2 v θ 2 + v r 2 = P ∞ - 2200 + 1225 2 33,8 2 + v r 2  

→ v r = 49,5 m s

  1. A intensidade será: v r = m r = m 40 → m = 1980 m 2 s .

Com as velocidades v r   e   v θ conhecidas, temos que o ângulo β   será:

β = tan - 1 ⁡ v r v θ = tan - 1 ⁡ 49,5 33,8 = 55,6 °

Em r=15m, calculamos v r = m r = 1980 15 = 132 m / s , uma velocidade absurdamente alta. E v θ = Γ 2 π r = 8500 2 π 15 = 90 m s , novamente uma velocidade muito alta, o que indica que provavelmente há um núcleo viscoso neste ponto. Agora, usamos Bernoulli novamente para calcular a pressão em r=15m:

P + 1225 2 132 2 + 90 2 = P ∞ → P = P ∞ - 15700 P a

Se assumirmos que P ∞ = P a t m = 101 k P a ,   t e m o s :

P a b s o l u t a = 85 k P a .

Resposta

  1. m = 1980 m 2 s
  2. P = P ∞ - 15700 P a
  3. β = 55,6 °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deixe o vetor G → ser dado por G → = 2 x z i → - 1 2 x 2 j → + z 2 k → . Calcule o divergente de G → , e simplifique o máximo possível. Existe algo de especial no seu resultado?
Quantas incógnitas há para um campo de escoamento tridimensional, em regime não permanente, incompressível, no qual as variações de temperatura são insignificantes? Liste as equações necessárias para
A regra do produto pode ser aplicada ao divergente do escalar f vezes o vetor G → como: ∇ → . f G → = G → . ∇ → f + f ∇ → . G → . Expanda ambos os lados desta equação em coordenadas cartesianas e veri
O produto exterior de dois vetores é um tensor de segunda ordem com nove componentes. Em coordenadas cartesianas, ele é:A regra do produto aplicada à divergência do produto aplicada ao divergente de d
Seja o vetor G → ser dado por G → = 4 x z i → - y 2 j → + y z k → e seja V o volume de um cubo de aresta unitária com seu vértice na origem, limitado por x = 0 a 1, y =0 a 1 e z = 0 a 1 (Fig. P9–9). A