Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 8
Três tubos forncecem água em regime permanente a para um tubo maior de saída mostrado na figura P3.8. A velocidade e a vazão de saída . Encontre:
- ;
- ;
Se sabemos que aumentando em aumentará em .
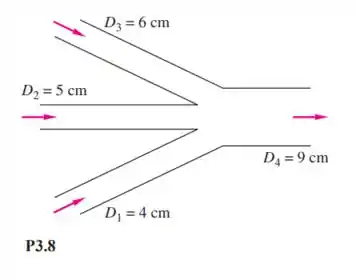
Passo 1
Bora para mais uma questãozinha jovem! Seguinte, como temos regime permanente, a soma de tudo que entra vai ser igual tudo que sai. Simples assim!
Mas lembrando que a vazão é igual o volume vezes a área:
Beleza! Até agora bem tranquilo né!
Passo 2
Bom, parece que alguns dados aí tão faltando né?! Vamos voltar no enunciado então, ele diz que:
Então:
Mas, está em . Portanto, precisamos passar para segundos:
Facilmente, então:
Já temos a letra (b).
Voltando naquela fórmula lá, a única icógnita é , portanto:
Passo 3
Então, encontramos:
E, na letra (c):
Bem tranquilo né!! Até a próxima!!
Resposta
Portanto:
- ;
- ;