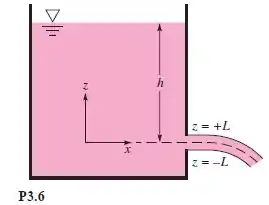
Quando um jato líquido, regido pela gravidade, sai de uma fenda em um tanque, como na Figura , uma aproximação para a distribuição de velocidade na saída é , onde é a profundidade da linha de centro do jato. Próximo à fenda, o jato é horizontal, bidimensional, e de espessura , como mostrado. Encontre uma expressão geral para a vazão volumétrica total que sai da fenda; em seguida, tome o limite do seu resultado para .

E aí, tudo bem? Bora resolver mais essa comigo!

Vamos matar essa questão rapidinho, primeiro precisamos lembrar que:

Para a nossa questão:

Essa integral é tranquila para resolvermos, assim:

Pra matar de vez essa questão, o problema nos pede o que aconteceria se , vamos lá.

Como e o termo dentro da raiz desaparece, assim:

Isso é tudo pessoal, conseguimos mais uma! \o/