Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 100
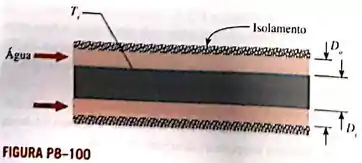
Um tubo anelar concêntrico tem diâmetro interno e externo de e , respectivamente. Um fluxo de água na vazão de escoa no tubo anelar com temperaturas médias de entrada e saída de e , repectivamente. A parede interna do tubo é mantida na temperatura de superfície constante de , enquanto a superfície externa do tubo é isolada. Determine o comprimento do tubo anelar.
Passo 1
Dados fornecidos:
Diâmetro interno do tubo anular:
Diâmetro externo do tubo anular:
Vazão mássica da água:
Temperatura da água de entrada:
Temperatura da água de saída:
Temperatura da superfície da parede do tubo interno:
Premissas:
1) Existem condições operacionais estáveis.
2) Propriedades são constantes.
3) Temperatura constante da superfície do tubo interno.
4) Superfície isolada do tubo externo.
5) Fluxo totalmente desenvolvido.
Passo 2
Agora, vamos calcular a temperatura média para obter as propriedades da água. Assim temos:
Com o valor da temperatura média, podemos obter as seguintes propriedades da água em na Tabela A-9.
Condutividade térmica:
Viscosidade dinâmica:
Calor específico:
Número e Prandtl:
Passo 3
Vamos começar calculando o número de Reynolds para encontrar o regime de fluxo usando a seguinte relação:
Aqui, é o diâmetro hidráulica que para um cilindro é , é a velocidade média do fluxo.
Podemos obter uma relação para a velocidade média do fluxo.
Aqui, é o diâmetro externo do tubo anular, é o diâmetro interno do tubo anular e é a taxa de fluxo de massa.
Substituindo a velocidade média em Reynolds, temos:
Substituindo os termos pelos dados fornecidos no enunciado, temos:
Como o número de Reynolds é menor que , o fluxo é considerado como fluxo laminar.
Passo 4
Da Tabela 8-4 denominada “Número de Nusselt para escoamento laminar completamente desenvolvido no espaço anular com uma superfície isotérmica e a outra adiabática” podemos obter o número de Nusselt para a relação .
Temos que a relação nos fornece o seguinte:
Para temos que o número de Nusselt é:
Podemos calcular o coeficiente de transferência de calor usando a seguinte relação:
Isolando o coeficiente de transferência de calor e substituindo , temos:
Substituindo os termos da equação pelos dados obtidos, temos:
Passo 5
O calor transferido pela água líquida é determinado usando a seguinte expressão;
Substituindo os termos da equação pelos dados obtidos, temos:
O comprimento do tubo anular é determinado pela seguinte expressão:
Aqui, é a temperatura da superfície do tubo interno, é a temperatura média da água na entrada, é a temperatura média da água na saída. Substituindo os termos da equação pelos dados fornecidos, temos:
O comprimento do tubo de anel concêntrico é .