Um aquecedor para promover a ebulição de um líquido saturado é formado por dois tubos concêntricos de aço inoxidável recheados com pó denso de nitreto de boro. Uma corrente elétrica é passada pelo tubo interno, gerando um aquecimento volumétrico uniforme A superfície exposta do tubo externo encontra-se em contato com o líquido e o fluxo térmico na ebulição é dado por
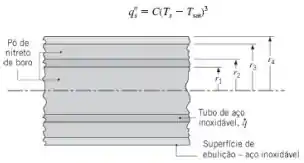
Teme-se que em operação à elevada potência os tubos de aço inoxidável se oxidem severamente se a temperatura for superior a ou então que o nitreto de boro se deteriore se sua temperatura exceder . Admitindo que a temperatura de saturação do líquido e a temperatura da superfície de ebulição sejam especificadas, deduza expressões para as temperaturas máximas nos tubos de aço inoxidável e no nitreto de boro Expresse seus resultados em termos de parâmetros geométricos das condutividades térmicas e dos parâmetros de ebulição
Passo 1
Nessa questão nós temos Tubos de aço inoxidável concêntricos embalados com pó denso de nitreto de boro. O tubo interno gera geração de calor enquanto a superfície do tubo externo é exposta ao fluxo de calor em ebulição. O circuito térmico é representado por:
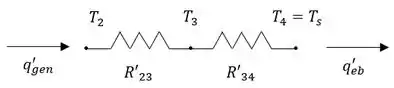
Com isso, queremos encontrar as expressões para a temperatura máxima nos tubos de aço inoxidável e no nitreto de boro
Passo 2
Para resolver essa questão vamos assumir condições em estado estacionário e transferência de calor unidimensional (cilíndrica) em estado estacionário em tubos e nitreto de boro.
e do circuito térmico mostrado acima, representam as resistências devidas ao nitreto de boro entre e e ao tubo externo de aço inoxidável, respectivamente. De um balanço energético geral temos,
Com os valores dados para , o aquecimento volumétrico necessário do tubo interno de aço inoxidável é,
Passo 3
Usando o circuito térmico, podemos escrever expressões para a temperatura máxima do aço inoxidável e nitreto de boro
Aço inoxidável: ocorre em e a distribuição de temperatura em um tubo radial dos raios interno e externo e é,
Onde as condições de contorno são,
Condição de contorno 1:
Passo 4
Condição de contorno 2:
Então,
Usando o circuito térmico, encontramos em termos dos parâmetros conhecidos .
Portanto, a temperatura máxima no tubo interno de aço inoxidável é,
Onde,
e
Passo 5
E para o nitreto de boro,
Nitreto de boro: acontece em . Então,
Conforme demonstrado acima para o tubo interno de aço inoxidável.