Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 40

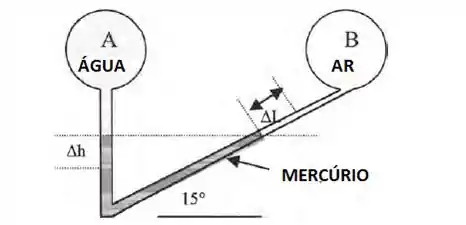
Na figura abaixo as pressões em A e B são as mesmas, 100 kPa. Se for colocada mais água em A para aumentar pA para 130 kPa, determine as novas posições dos meniscos de mercúrio. O tubo de conexão tem um diâmetro uniforme de 1cm. Considere que não haja mudança nas densidades dos fluidos.

Passo 1

Primeira coisa é analisar a física do problema. Considerando que o diâmetro do tubo é constante, ao se adicionar água no sistema, uma certa quantidade de mercúrio irá descer no lado onde está o recipiente com água, que vamos chamar de Δ h . Essa quantidade irá deslocar um volume igual do lado direito, que vamos chamar de Δ L . Portanto já tiramos daqui que:

Δ L = Δ h

Lembrando de tomar as densidades dos fluidos:

ρ á g u a = 979   k g / m ³

ρ H g = 13310   k g / m ³

Passo 2

Agora vamos aplicar a hidrostática a partir da interface entre mercúrio e ar, beleza?

P B + ρ H g g Y + ρ á g u a g H = P A

Vale lembrar aqui que toda vez que você ver um tubo inclinado, pra conhecer a pressão que o fluido ali exerce sob um ponto, você precisará calcular qual é a altura vertical desse tubo.

Passo 3

Vamos calcular então quem seria nosso Y, que é a altura vertical de mercúrio que subiu após a adição de água, beleza?

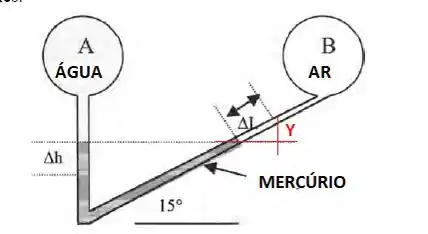
Note que a altura vertical nova será dada pela função trigonométrica do seno, concorda?

s e n 15 ° = Y Δ L → Y = Δ L   s e n 15 °

Passo 4

Com a adição de água, descemos uma altura Δ h no nível de água (porque agora temos mais água), podemos então escrever a nossa equação hidrostática da seguinte maneira:

P B + ρ H g g Δ L   s e n θ + Δ h = P A + ρ á g u a g ( Δ h + Δ L   s e n θ )

100000 + 133100 Δ h 1 + s e n 15 ° - 9790 Δ h 1 + s e n 15 ° = P A = 130000

Resolvendo para Δ h → Δ h = 0,193 m

Isso significa que o mercúrio vai subir 0,193m de altura do lado direito e a água vai descer essa mesma altura.

Resposta

Δ h = 0,193 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

For the traditional equal-level manometer measurement inFig. E2.3, water at 208C flows through the plug devicefrom a to b. The manometer fl uid is mercury. If L 5 12 cmand h 5 24 cm, (a) what is the p
For gases that undergo large changes in height, the linearapproximation, Eq. (2.14), is inaccurate. Expand the troposphere power-law, Eq. (2.20), into a power series, andshow that the linear approxima
If the absolute pressure at the interface between water andmercury in Fig. P2.16 is 93 kPa, what, in lbf/ft2, is (a) thepressure at the surface and (b) the pressure at the bottom ofthe container?
A small submarine, with a hatch door 30 in in diameter,is submerged in seawater. (a) If the water hydrostaticforce on the hatch is 69,000 lbf, how deep is the sub?(b) If the sub is 350 ft deep, what i
A storage tank, 26 ft in diameter and 36 ft high, is filledwith SAE 30W oil at 208C. (a) What is the gage pressure,in lbf/in2, at the bottom of the tank? (b) How does your result in (a) change if the