Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 120
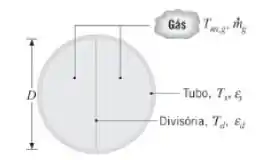
O tubo de chama de um sistema de aquecimento de água é constituído por um longo duto circular com diâmetro D = 0,07 m e temperatura Ts = 385 K, através do qual gases de combustão escoam a uma temperatura de Tm,g = 900 K. Para melhorar a transferência de calor do gás para o tubo, uma fina divisória é inserida ao longo do plano central do tubo. Considere que os gases tenham as propriedades termofísicas do ar e um comportamento
radiante não participante.
- Sem a divisória e com uma vazão do gás de , qual é a taxa de transferência de calor para o tubo por unidade de comprimento, q′?
- Para uma vazão do gás de e emissividades de εs = εd = 0,5, determine a temperatura da divisória, Td, e a taxa de transferência de calor total para o tubo, q′.
- Para , e emissividades equivalentes, εd ≡ εs ≡ ε, calcule e represente graficamente Td e q′ como funções de ε para 0,1 ≤ ε ≤ 1,0. Para e emissividades equivalentes, represente graficamente as contribuições convectiva e radiante para q′ como funções de ε
Passo 1
É isso ai galerinhaaa !! Vamos continuando?
Bom, antes de qualquer coisa, a letra (a) nos pediu qual a taxa de transferência de calor para o tubo por unidade de comprimento, , quando não temos a parede, ok?
Se não temos a parede, a transferência de calor ocorre apenas por convecção!
Neste caso:
Então:
O problema nos disse que:
Só precisamos então do coeficiente convectivo, certo?
Para isso precisamos primeiro do Reynolds:
Para o ar está a temperatura de 900 K, vamos olhar na Tabela A – 4:
Quando o ar está a 385 K:
Para o primeiro caso:
Para o coeficiente convectivo:
Substituindo:
E calculando o calor:
E essa é a letra (a) !! Bora continuar?
Passo 2
Bom, na letra (b) nós teremos a troca de calor por convecção e radiação !
Para o novo é o calor convectivo, precisamos achar o novo coeficiente convectivo, já que agora temos apenas metade do tubo passamos a analisar um tubo não- circular!
Para este caso o Reynolds muda um pouco:
Dado que:
No Reynolds:
Substituindo:
Para o coeficiente convectivo:
Substituindo:
A fórmula para o calor convectivo fica um pouco diferente por causa da parede:
Substituindo:
Passo 3
Para o calor radiante temos:
O que nós sabemos é que:
E a razão entre as áreas da parede e da superfície nós podemos achar:
Só substituir agora:
Para achar a temperatura da parede nós vamos igualar estes dois calores:
E resolvendo com auxílio de um software:
Achamos uma resposta, mas a letra (b) não pediu só isso, certo? Também queremos a taxa de transferência de calor total para o tubo, q’.
Como temos fluxo radiante e convectivo:
Abrindo a equação:
E substituindo:
Bom, é importante vocês lembrarem aqui que esse é o fluxo para metade do tudo, não é?
Se queremos para o tubo inteiro:
E chegamos ao fim da letra (b), bora seguir porque não acabamos !!
Passo 4
Na letra (c) nós queremos representar e para com ε variando de 0,1 até 1.
E para isso vamos usar novamente um software, não é?
E chegamos ao fim de mais umaaa !!
