Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 118
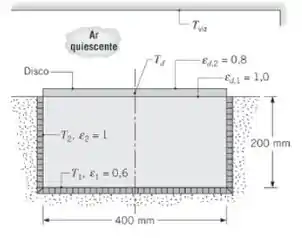
O lado inferior de um disco com 400 mm de diâmetro é aquecido por um forno elétrico, enquanto o lado superior está exposto ao ar ambiente quiescente e a uma vizinhança, ambos a 300 K. O forno radiante (convecção desprezível) é de construção circular, com a superfície
inferior (ε1 = 0,6) e a superfície lateral cilíndrica (ε2 = 1,0) mantidas a T1 = T2 = 500 K. A superfície do disco voltada para o forno radiante é negra (εd,1 = 1,0), enquanto a superfície superior tem uma emissividade de εd,2 = 0,8. Suponha que as superfícies do disco e do forno sejam cinzas e difusas.
- Determine a taxa de transferência de calor líquida para o disco, , quando Td = 400 K.
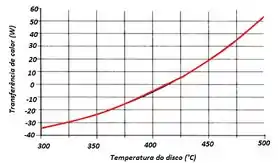
- Represente graficamente qliq,d como uma função da temperatura do disco para 300 ≤ Td ≤ 500 K, com todas as demais condições permanecendo as mesmas. Qual é a temperatura do disco em regime estacionário?
Passo 1
É isso ai galerinhaaa !! Vamos continuando?
Bom, a letra (a) nos pede para achar a taxa de transferência de calor líquida para o disco, , ok?
O disco está perdendo calor radiante com a superfície e convectivo com o ar, além de perder calor para a superfície interna:
Vamos olhar cada um mais de perto! Começando pelo calor radiante:
Lembrando que:
Substituindo:
Agora que achamos o radiante vamos para os próximos!!
Passo 2
Para o calor convectivo:
Só nos falta o coeficiente convectivo, sabendo que:
Neste caso:
Para achar as propriedades do ar nós precisamos da temperatura média:
Assumindo que a temperatura seja próxima a e olhando na Tabela A – 4:
Substituindo:
Quando podemos usar:
Substituindo:
Colocando no calor:
Passo 3
Para o espaço interno, o fluxo radiante é calculado por:
A área nós já conhecemos, certo?
Como as superfícies 2 e 3 são negras, as potências emissivas são calculadas por:
Lembrando que:
Substituindo:
Nós ainda não temos os fatores de forma, vamos acha-lo?
Olhando a figura abaixo para os discos coaxiais:
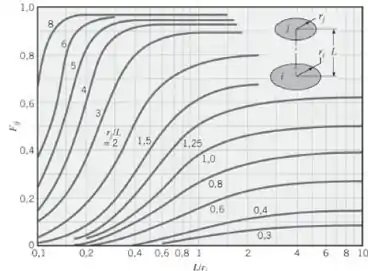
Sabendo que:
Então:
Olhando no gráfico, o fator de forma entre o ambiente e a superfície interna:
Aplicando o somatório para a superfície 3:
Temos quase tudo que precisamos, só nos falta
Passo 4
Para achar nós podemos usar a seguinte relação:
Substituindo o que temos:
Agora sim!!
E o calor líquido:
Agora sim !! Chegamos ao da letra (a) !!
Passo 5
A letra (b) nos pede para representar graficamente como uma função da temperatura do disco para , com todas as demais condições permanecendo as mesmas.
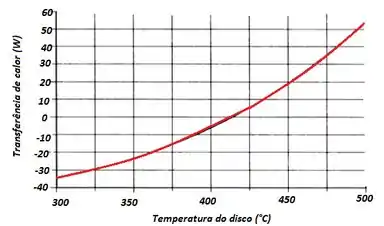
A letra (b) também nos pede a temperatura do disco em regime estacionário, ou seja, quando
Quando substituímos no somatório do passo anterior e utilizamos um software para resolver, obtemos que:
E finalizamos mais umaa !!
Resposta
