Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 95
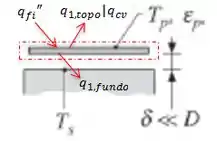
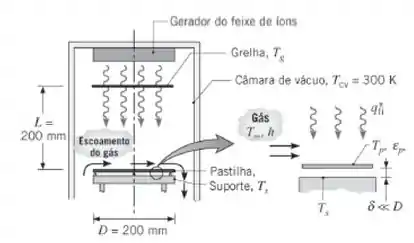
Uma ferramenta para o processamento de pastilhas de silício está posicionada no interior de uma câmara de vácuo cujas paredes são negras e mantidas a , por um refrigerante. A fina pastilha de silício é montada próxima a um suporte, mas sem tocá-lo, que é aquecido eletricamente e mantido a uma temperatura . A superfície do suporte voltada para a pastilha é negra. A temperatura da pastilha é e a sua superfície é difusa e cinza, com uma emissividade . A função da grelha, uma fina folha metálica posicionada coaxialmente à pastilha e com um diâmetro igual ao da pastilha, é controlar a potência do feixe de íons que atinge a pastilha. A superfície da grelha é negra, com uma temperatura de . O efeito do feixe de íons que colide na pastilha é o de fornecer um fluxo térmico uniforme de . A superfície superior da pastilha é submetida ao escoamento de um gás de processo com e . Como o espaço entre a pastilha e o suporte, δ, é muito pequeno, o escoamento do gás de processo nessa região pode ser desprezado.
- Represente a pastilha esquematicamente, mostrando uma superfície de controle e todos os processos térmicos relevantes.
- Efetue um balanço de energia na pastilha e determine a temperatura do suporte .
Passo 1
Animados para seguir que eu sei, não é?
A letra (a) é relativamente simples, nos pede para representar os processos térmicos relevantes para a pastilha, tranquilo?
Vamos ver o que temos atuando então?
Primeiro galera, o gerador de feixe de íons está gerando um fluxo de calor, , a pastilha tem calor sendo removido pela parte superior, , e inferior, O gás também remove calor da pastilha, mas por convecção, .
Vamos pegar a ampliação do desenho que já temos e colocar tudo isso?
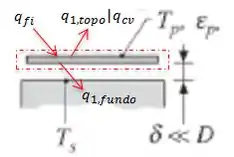
E a letra (a) acabou !
Passo 2
Agora na letra (b) nós precisamos fazer um balanço de energia na pastilha e determine a temperatura do suporte !
Se já temos a figura ficou fácil:
Substituindo o que já sabemos:
Para o feixe de íons nós precisamos levar em conta a área da pastilha, certo?
Sabemos que:
Então:
Convecção também vocês já estão carecas de saber, não é?
Sabemos que:
E substituindo:
Já temos duas, não é? Mas vamos achar as outras !!
Passo 3
A taxa removida no compartimento entre a parte do fundo da pastilha e da superfície pode ser escrita como mostra a Tabela 13.3:
Lembrando do que ainda não usamos:
Substituindo:
Agora, para a taxa de transferência de calor removida do topo da pastilha nós usamos aquela fórmula que já até decoramos:
Onde é a potência emissiva, a radiosidade, a área e a emissividade da superfície i.
Vamos dar uma olhada na equação aberta?
s:
Para calcular as potências emissivas:
Como a câmara de vácuo e a grade são negras:
Lembrando que:
Então:
Então nós só precisamos dos fatores de forma!!
Passo 4
Para discos paralelos coaxiais, como a pastilha e a grade nós podemos usar a figura abaixo:
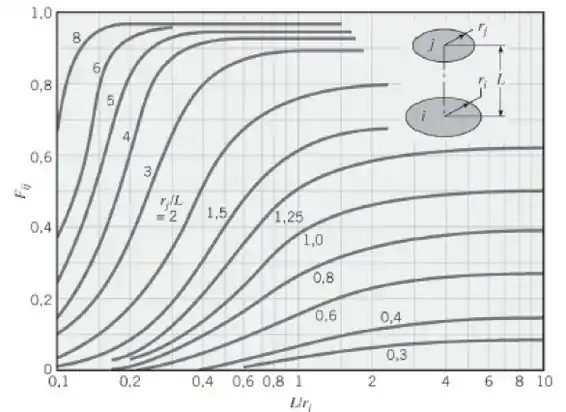
Se:
Fazendo a razão:
Olhando no gráfico:
Fazendo o somatório para a pastilha:
Substituindo:
Agora que nós temos a radiosidade ficou fácil achar a transferência de calor usando a equação no Passo 3:
E agora?
Colocamos tudo isso no balanço:
Legal, não foi ?!
