Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 116
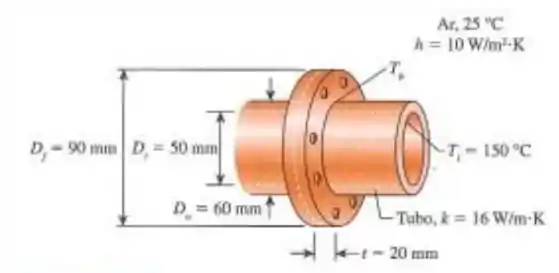
Tubos com diâmetros interno e externo de 50 mm e 60 mm, respectivamente, são usados para transportar vapor superaquecido em uma fábrica. Os tubos com condutividade térmica de são ligados entre si por flanges com espessura combinada de 20 mm e diâmetro externo de 90 mm. A condição do ar ao redor dos tubos tem uma temperatura de 25°C e o coeficiente de transferência de calor por convecção de . Considerando que a temperatura da superfície interna do tubo é mantida a uma temperatura constante de 150°C, determine a temperatura na base do flange e a taxa de perda de calor através do flange.
Passo 1
Boom galera, o que temos aqui??
A primeira coisa é saber a temperatura na base do flange, ou melhor, a temperatura na superfície do tubo, certo?
Se é assim, nós temos apenas duas resistências atuando aqui, a convectiva externa e a condutiva apresentada pelo tubo:
Já sabemos como calcular as resistências, só precisamos das áreas.
Para a área externa nós levamos em consideração o diâmetro externo do tubo e levando em conta 1 metro de tubo:
Passo 2
Agora vamos calcular as resistências:
Como todas estão em série a resistência total será:
Com a resistência nós podemos achar qual a taxa que calor atravessa o tubo:
Substituindo:
Como a variação em graus Celsius e kelvin é a mesma:
Mas não respondemos a pergunta, queremos saber qual a temperatura na superfície do tubo.
Se levarmos em conta que a transferência de calor não muda, e analisando somente a resistência convectiva externa nós podemos transformar a equação do calor em algo que resolva nossa questão:
Substituindo:
É isso aii! Achamos a primeira resposta, agora vamos precisar da segunda !!
Passo 3
Bora achar a transferência de calor??
Antes de qualquer coisa nós precisamos analisar a eficiência desta aleta, ok?
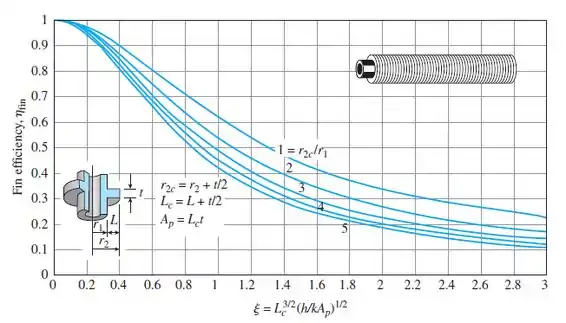
E para achar a eficiência vamos usar o gráfico que foi dado no livro:
Vamos precisar achar a razão e
Começando pela razão e lembrando que:
Então:
Substituindo:
E quanto ao
Se:
Então:
Substituindo:
Analisando o gráfico para e , a eficiência será próxima de 0,98.
Então:
Achamos uma das respostas que precisamos mais ainda não terminamos a letra b!!
Passo 4
Agora nós queremos a taxa de transferência de calor. E para isso basta nós usarmos a fórmula que já nos foi dado, certo?
Não se lembram?
Eu mostro pra vocês:
Como nós temos uma eficiência de 98% a fórmula vai ficar um pouco diferente:
Isso porque nós precisamos levar em conta essa eficiência para achar uma resposta adequada ao problema, beleza?
Nós temos quase tudo o que precisamos:
Mas falta a área!!
Só que para calcula-la nós podemos usar uma formulazinha também:
Como estamos falando da aleta, o raio 2 será o raio maior e o raio 1 será o raio do orifício, tudo bem até aqui??
Agora que sabemos a fórmula e os dados é só substituir:
Beleza!!
Se temos tudo o que precisamos agora é só calcular a taxa para transferência de calor:
Como a variação em graus Celsius e em kelvin é a mesma:
Agooora sim !! Achamos tudo o que precisávamos !