Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 32
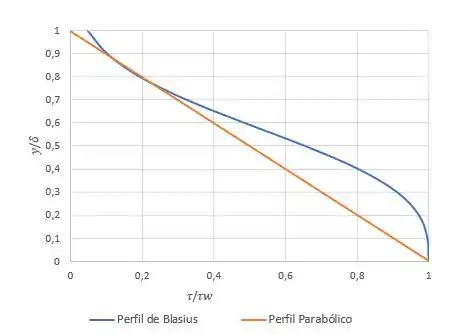
Usando os resultados numéricos obtidos por Blasius (Tabela 9.1), avalie a distribuição de tensão de cisalhamento em uma camada limite laminar sobre uma placa plana. Trace versus . Compare com os resultados deduzidos a partir do perfil de velocidade aproximado parabólico dado no Problema 9.10.
Passo 1
A equação de um perfil parabólico tem essa carinha:
O que o enunciado está pedindo, na real, é para a gente achar, para esse perfil e para os dados de Blasius, uma relação entre e (uma equação que relaciona os dois). Com isso a gente acha duas funções. Nosso objetivo é plotar os gráficos delas para comparar.
Passo 2
Vamos começar achando a relação de e para o caso de Blasius. Para ele:
A gente pode lembrar que a lei da viscosidade para um fluído de Newton diz que:
Dá para derivar nossa expressão de na expressão da tensão de de cisalhamento
Usando a regra da cadeia:
Passo 3
Achamos uma relação entre e . Precisamos achar quem é , logo quem é .
Lembrando que é o cisalhamento na parede da placa, ou seja, onde :
Agora só dividir por :
Pela tabela dos resultados numéricos a gente sabe , por isso nossa expressão fica:
A gente pode dizer que em , , assim dá para escrever:
Com isso, a nossa primeira função fica com essa carinha:
Podemos plotar esse gráfico variando os valores de , pela tabela dos resultados numéricos de Blasius.
Passo 4
Agora precisamos achar a nossa expressão para o caso do perfil parabólico. Vamos usar o mesmo raciocínio:
Passo 5
Como , acontece em :
Dividindo uma expressão pela outra:
Prontinho, agora é só variar o para plotar nosso gráfico.
Passo 6
Temos então a expressão para o caso de Blasius, onde a gente precisa usar os resultados numéricos de para plotar o gráfico:
E temos a expressão para o caso do perfil parabólico, onde só precisamos variar o :
Plotando essas duas funções juntas para comparar:
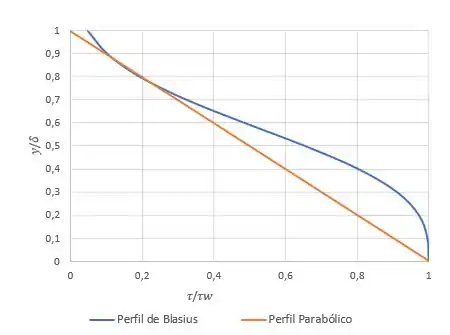
Resposta
