Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas Abrangentes - Ex. 4

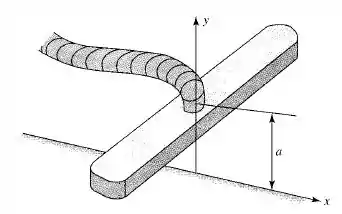
Use o modelo de escoamento potencial para aproximar o escoamento do ar de sucção de um aspirador de pó através de um adaptador com fenda bidimensional, como na figura abaixo. No plano xy através da linha de centro do adaptador, modele o escoamento por meio de um sumidouro de intensidade (-m) bidimensional (com seu eixo na direção z) a uma altura “a” acima do piso. (a) Trace as linhas de corrente e localize quaisquer pontos de estagnação do escoamento. (b) Encontre a intensidade da velocidade V(x) ao longo do piso em termos dos parâmetros “a” e “m”. (c) Considere a pressão p ∞ bem longe, onde a velocidade é zero. Defina uma escala de velocidade U = m / a . Determine a variação do coeficiente de pressão adimensional, C p = ( p - p ∞ ) / ( ρ U 2 / 2 ) , ao longo do piso. (d) O aspirador de pó é mais efetivo onde o C p é mínimo, isto é, onde a velocidade é máxima. Encontre as posições de coeficiente de pressão mínimo ao longo do eixo (x).

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

(a) O “chão” é criado por um sumidouro em (0, +a) e um termo sumidouro imagem em (0,-a), exatamente como na figura 8.17a do livro. Não há ponto de estagnação na origem, certo? As linhas de corrente são mostradas abaixo como ficaram hehe

Passo 2

(b) Em qualquer ponto x ao longo da parede, a velocidade V é o somatório dos fluxos no ponto (0,-a)

V = 2 v r , s u m i d o u r o c o s θ = 2 m x r x r = 2 m x x 2 + a 2 = V a o   l o n g o   d a   p a r e d e

Passo 3

(c) Usando a equação de Bernoulli para calcular o coeficiente de pressão ao longo da parede, temos que:

C p = p - p ∞ 1 2 ρ U 2 = 1 2 ρ U ∞ 2 - V 2 1 2 ρ U 2 = - V 2 U 2 → C p , p a r e d e = - 4 x 2 a 2 x 2 + a 2 2

Passo 4

(d) O coeficiente de pressão mínimo é encontrado quando nós aplicamos a derivada na equação que encontramos no passo 3 e igualamos a zero, certo?

d C p d x = 0 → d d x - 4 x 2 a 2 x 2 + a 2 2 = 0

Note que para isso acontecer, precisamos que x 2 = a 2 , ou seja, x = ± a

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Explique as diferenças fundamentais entre um domínio de escoamento e um volume de controle.
Quantas incógnitas há para um campo de escoamento tridimensional, em regime não permanente, compressível, no qual as variações de temperatura e densidade são significativas? Liste as equações necessár
O teorema do divergente é expresso como: ∫ V ∇ →. G → d V = ∮ A G →. n → d A onde G → é um vetor, V é um volume e A é a área da superfície que delimita e define o volume. Expresse o teorema do diverge
Uma expansão em séries de Taylor da função f ( x ) ao redor de alguma posição x 0 é dada por: f x 0 + d x = f x 0 + d f d x x = x 0 d x + 1 2 ! d 2 f d x 2 x = x 0 d x 2 + 1 3 ! d 3 f d x 3 x = x 0 d
Use a regra do produto do Problema 9-11 para demonstrar que ∇ → . ρ V → V → = V → ∇ →. ρ V → + ρ ( V→. ∇ → ) V → .