Em uma usina hidrelétrica a água a é fornecida para a turbina a uma taxa de através de um tubo de ferro fundido com de comprimento e de diâmetro. A diferença de elevação entre a superfície livre do reservatório e a descarga da turbina é de , e a eficiência combinada de turbina-gerador é de . Desprezando as perdas menores por conta da razão grande entre comprimento e diâmetro, determine a saída de potência elétrica dessa usina.

Desprezando as perdas menores, podemos utilizar a equação de energia (que é a de Bernoulli, com alguns acréscimos). Assim, estabelecendo os pontos de análise e , temos:

Pelo diagrama, os pontos e são expostos a atmosfera, ou seja, . Além disso, o nosso ponto de referência é em e as velocidade são praticamente desprezíveis, ou seja, . Por ultimo, não temos bomba, então . Assim, temos:

Agora, vamos aos cálculos das variáveis. A velocidade é:

A rugosidade dos tubos sobre o diâmetro é:

Calculando o número de Reynolds:

Com esses resultados, vamos determinar o fator de atrito através do diagrama de Moody:

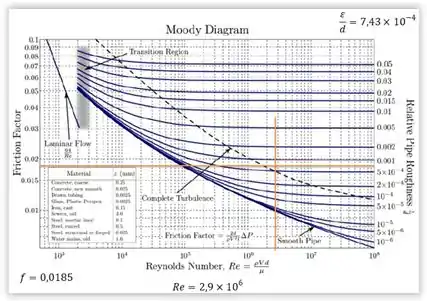
Assim, o fator de atrito é .

Voltando a expressão que calculamos no passo , calculamos a perda de carga:

Substituindo:

A potencia real da turbina é dada por:

Assim, com a eficiência turbina-gerador, temos:

Prontinho!!