Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 56

Vapor saturado oriundo de um processo químico condensa a uma taxa baixa sobre a superfície interna de um recipiente cilíndrico vertical com paredes finas, comprimento L e diâmetro D. A parede do recipiente é mantida a uma temperatura uniforme T s pelo escoamento de água fria ao redor da sua superfície externa.

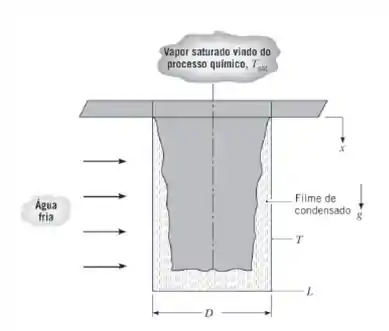
Deduza uma expressão para o tempo, t e , necessário para o enchimento completo do recipiente com o condensado, admitindo que o filme de condensado seja laminar. Expresse seu resultado em termos de D, L, T s a t - T s , g e das propriedades do fluido pertinentes.

Passo 1

Beleza! Sabemos então que a vazão mássica é dada pela razão entre a massa que sai/entra do sistema e o intervalo de tempo em que isso ocorre. Escrevendo isso na forma diferencial, temos:

m ˙ = d M d t

No nosso caso m ˙ é a taxa de condensação e M é a massa do recipiente. Que, com o auxílio da figura dada no enunciado, é dada por:

M = ρ l V = ρ l A h

Temos que a área será a área correspondente a uma seção circular. Já a altura será variável, pois conforme o recipiente for enchendo, ela irá se alterar. Dessa forma, com a orientação do eixo x da forma com que foi dada no enunciado, a equação para a massa se torna:

M = ρ l π D 2 4 L - x → M = ρ l π D 2 4 L - x

Agora, sabendo que a taxa de condensado pode ser dada pela equação 10.34, que é:

m ˙ = q h f g '

Substituindo a expressão da lei de resfriamento de Newton para a taxa de transferência de calor, teremos:

m ˙ = q h f g ' → m ˙ = h s A s T s a t - T s h f g '

Passo 2

Agora, para encontrar o coeficiente de convecção da equação do passo 1, nós precisamos utilizar a equação 10.31, calculando para o comprimento x , teremos:

h s = 0,943 g ρ l ρ l - ρ v k l 3 h f g ' μ l T s a t - T s x 1 4

Agora, a área superficial de contato A s da equação do passo 1 também dependerá da altura do recipiente, de tal modo que:

A s = π D x

Então, substituindo essas duas expressões na equação para a vazão mássica, chegamos em:

m ˙ = 0,943 g ρ l ρ l - ρ v k l 3 h f g ' μ l T s a t - T s x 1 4 π D x T s a t - T s h f g '

Agora, vamos substituir essa expressão, juntamente com a expressão para a massa na primeira equação do passo 1, onde definimos a vazão mássica, dessa forma, chegaremos em:

0,943 g ρ l ρ l - ρ v k l 3 h f g ' μ l T s a t - T s x 1 4 π D x T s a t - T s h f g ' = d d t ρ l π D 2 4 L - x

Então, do lado direito da equação, derivando a expressão no tempo, temos que o primeiro termo, multiplicado por L, será igual a zero, pois ele não depende do tempo. Já o segundo que multiplica por x deixaremos em função do tempo, pois estamos interessados justamente no tempo t e de enchimento, então a equação acima se torna:

0,943 g ρ l ρ l - ρ v k l 3 h f g ' μ l T s a t - T s x 1 4 π D x T s a t - T s h f g ' = - ρ l π D 2 4 . d x d t

Passo 3

Agora precisamos separar as variáveis x e t para poder integrar a expressão, então, manipulando a expressão anterior, chegamos em:

0,943 g ρ l ρ l - ρ v k l 3 h f g ' μ l T s a t - T s x 1 4 π D x T s a t - T s h f g ' = - ρ l π D 2 4 . d x d t

0,943 g ρ l ρ l - ρ v k l 3 h f g ' μ l T s a t - T s 1 4 π D x 3 4 T s a t - T s h f g ' = - ρ l π D 2 4 . d x d t

3,772 π T s a t - T s g ρ l ρ l - ρ v k l 3 h f g ' 1 4 h f g ' ρ l π D μ l T s a t - T s 1 4 d t = - x - 3 4 d x

Então, integrando essa expressão de x = L até zero, no tempo de 0 até o tempo de enchimento, teremos:

∫ 0 t e 3,772 π T s a t - T s g ρ l ρ l - ρ v k l 3 h f g ' 1 4 h f g ' ρ l π D μ l T s a t - T s 1 4 d t = ∫ L 0 - x - 3 4 d x

Resolvendo as integrais, teremos:

3,772 π T s a t - T s g ρ l ρ l - ρ v k l 3 h f g ' 1 4 h f g ' ρ l π D μ l T s a t - T s 1 4 t 0 t e = - 4 x 1 4 L 0

Substituindo os limites de integração, teremos:

3,772 π T s a t - T s g ρ l ρ l - ρ v k l 3 h f g ' 1 4 h f g ' ρ l π D μ l T s a t - T s 1 4 t e = 4 L 1 4

E, isolando o tempo de enchimento, chegamos em:

t e = 4 L 1 4 h f g ' ρ l π D μ l T s a t - T s 1 4 3,772 π T s a t - T s g ρ l ρ l - ρ v k l 3 h f g ' 1 4

Resposta

t e = 4 L 1 4 h f g ' ρ l π D μ l T s a t - T s 1 4 3,772 π T s a t - T s g ρ l ρ l - ρ v k l 3 h f g ' 1 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

139 - Termômetros cilíndricos de bulbo seco e de bulbo úmido estão instalados em um duto de grande diâmetro com o objetivo de obter a temperatura T ∞ e a umidade relativa ∅ ∞ do ar úmido que escoa atr
147 - A evaporação de gotículas de combustíveis líquidos é frequentemente estudada em laboratório usando-se a técnica da esfera porosa, na qual o combustível é alimentado a uma taxa que é suficiente a
148 - Seja um sistema de condicionamento de ar composto por um feixe de tubos montado normal ao ar que escoa no interior de um duto a uma vazão mássica de m ˙ a( k g / s ) . Um refrigerante escoando a
144 - Como descrito no Problema 7.84, a segunda etapa na engenharia tecidual é a semeação da superfície superior da base de sustentação com células humanas que em seguida crescem para o interior dos p
Considere a perda de massa na superfície de uma placa plana lisa e molhada, em função da convecção forçada à pressão atmosférica. A placa possui um comprimento de 0,5m e uma largura de 3m . Ar seco, a