Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 25

Considere a superfície metálica do Exemplo 12.7. Medições adicionais da emissividade hemisférica espectral fornecem uma distribuição espectral que pode ser aproximada como a seguir:

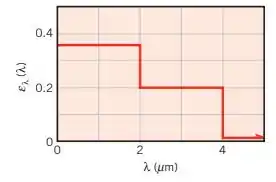
(a) Determine os valores correspondentes da emissividade hemisférica total ε e do poder emissivo total E a 2000   K .

Passo 1

Bora resolver mais uma questão juntos?

Então, fique de olho para não se perder!

Temos que a emissividade total, ε , pode ser determinada a partir da emissividade espectral hemisférica, ε λ , utilizando a seguinte equação:

ε T = ∫ 0 ∞ ε λ λ E λ , b λ , T d λ E b T

ε T = ε 1 ∫ 0 2   μ m E λ , b λ , T d λ E b T + ε 2 ∫ 2   μ m 4   μ m E λ , b λ , T d λ E b T

Ou pela equação:

ε T = ε 1 F 0 → λ 1 + ε 2 F 0 → λ 2 - F 0 → λ 1

Passo 2

Pela Tabela 12.2. obtemos:

λ 1 = 2   μ m ; T = 2000 K ; λ 1 T = 4000   μ m ⋅ K e F 0 → λ 1 = 0,481 ;

λ 1 = 4   μ m ; T = 2000 K ; λ 2 T = 8 000   μ m ⋅ K e F 0 → λ 2 = 0 , 856 .

Calculando a emissividade hemisférica total:

ε T = 0,36 ⋅ 0,481 + 0,20 ⋅ 0,856 - 0,481

ε T = 0,25

Por fim, calculando o poder emissivo total:

E 2000   K = ε 2000   K ⋅ E b 2000   K

E 2000   K = 0,25 ⋅ 5,67 × 10 - 8 ⋅ 2000 4

E 2000   K = 2,27 × 10 5   W / m 2

E assim a gente termina a nossa questão.

Te espero na próxima, até lá!

Resposta

ε T = 0,25

E 2000   K = 2,27 × 10 5   W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um material que é cinza, mas seletivo direcionalmente com α θ θ ,ϕ = 0,5 1–c o s ϕ . Determine a absortividade hemisférica α quando um fluxo solar colimado irradia a superfície do material n
Quatro superfícies difusas, que apresentam as características espectrais mostradas nas figuras, se encontram a 300 K e estão expostas à radiação solar.Quais das superfícies podem ser aproximadas como
A transmissividade espectral de um filme de polímero com 50μ m de espessura é medida no intervalo de comprimentos de onda 2,5μ m≤λ≤15μ m . A distribuição espectral pode ser aproximada por τ λ=0,80 par
Considere um grande forno com paredes opacas, difusas e cinzas, que se encontram a 3000K e cuja emissividade é de 0,85 . Um pequeno objeto difuso e espectralmente seletivo é mantido no interior do for
A absortividade espectral α λ e a refletividade espectral ρ λ de um material difuso espectralmente seletivo são mostradas a seguir.(a) Esboce a transmissividade espectral τ λ .(b) Se irradiação solar