Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 34

Um pequeno objeto opaco e difuso, a T s = 5 00   K , está suspenso em um grande forno cujas paredes internas estão a T f = 2 5 00   K . As paredes são difusas e cinzas, e têm uma emissividade de 0 , 37 . A emissividade hemisférica espectral da superfície do pequeno objeto é dada a seguir.

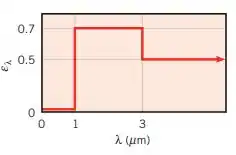
(a) Determine a emissividade total e a absortividade total da superfície.

(b) Avalie o fluxo radiante refletido e o fluxo radiante líquido para a superfície.

(c) Qual é o poder emissivo espectral em λ = 2   μ m ?

(d) Qual é o comprimento de onda λ 1 2 para o qual metade da radiação total emitida pela superfície se encontra na região espectral λ ≥ λ 1 2 ?

Passo 1

E aí, vem comigo resolver essa questão?

Bora lá então!

Letra a)

A emissividade do objeto pode ser obtida pela seguinte equação:

ε T s = ∫ 0 ∞ ε λ λ E λ , b ( λ , T s ) d λ E b T = ε 1 F 0 → 3   μ m - F 0 → 1   μ m + ε 2 1 - F 0 → 3   μ m

Com:

λ 1 T s = 500   μ m ⋅ K

λ 2 T s = 1500   μ m ⋅ K

F 0 → 1   μ m = 0

F 0 → 3   μ m = 0,084

Assim:

ε T s = 0,7 ⋅ ( 0,084 - 0 ) + 0,5 ⋅ 1 - 0,084

ε T s = 0,517

Calculando a absortividade total da superfície:

α ( T f ) = ∫ 0 ∞ α λ λ G λ λ d λ ∫ 0 ∞ G λ λ d λ = ∫ 0 ∞ α λ λ E λ , b λ , T f d λ E b T f

α T f = α 1 F 0 → 3   μ m - F 0 → 1   μ m + α 2 1 - F 0 → 3   μ m

Com:

λ 1 T s = 25 00   μ m ⋅ K

λ 2 T s = 75 00   μ m ⋅ K

F 0 → 1   μ m = 0 , 1615

F 0 → 3   μ m = 0,8343

Assim:

α T f = 0,7 ⋅ ( 0,8343 - 0,1615 ) + 0,5 ⋅ 1 - 0,8343

α T f = 0,554

Passo 2

Letra b)

Calculando a fluxo radiante refletido

G r e f = ρ G = 1 - α E b T f = 1 - α σ T f 4

G r e f = 1 - 0,554 ⋅ 5,67 × 10 - 8 ⋅ 2500 4

G r e f = 9,88 × 10 5   W / m 2

Calculando o fluxo radiante líquido para a superfície:

q r a d ' ' = G - ρ G - ε E b T f = α E b T f - ε E b T s

q r a d ' ' = σ α T f 4 - ε T s 4

q r a d ' ' = 5,67 × 10 - 8 ⋅ 0,554 ⋅ 2500 4 - 0,517 ⋅ 500 4

q r a d ' ' = 1,225 × 10 5   W / m 2

Passo 3

Letra c)

Para λ = 2   μ m , temos:

λ T s = 1000   μ m ⋅ K

Pela Tabela 12.2:

I λ , b λ , T σ T 5 = 0,1185 × 10 - 5

I λ , b λ , T = 5,67 × 10 - 8 ⋅ 500 5 ⋅ 0,1185 × 10 - 5

I λ , b λ , T = 2,1   W / m 2

Bora para o último!

Passo 4

Letra d)

Pela Tabela 12.2:

F 0 → λ = 0,5

Que corresponde:

λ T s ≅ 4100   μ m ⋅ K

λ = 4100 500

λ = 8,2   μ m

Te espero na próxima questão!

Resposta

a )   ε T s = 0,517 ;   α T s = 0,554

b )   G r e f = 9,88 × 10 5   W / m 2 ;   q r a d ' ' = 1,225 × 10 5   W / m 2

c )   I λ , b λ , T = 2,1   W / m 2

d )   λ = 8,2   μ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

45 - Um termômetro de radiação é um instrumento que responde a um fluxo radiante em um intervalo espectral estabelecido e é calibrado para indicar a temperatura de um corpo negro que produz o mesmo fl
50 - Um pequeno objeto opaco e difuso, a T s = 400K , está suspenso em um grande forno cujas paredes internas estão a T f = 2000K . As paredes são difusas e cinzas, e têm uma emissividade de 0,20 . A
58 - Considere uma superfície difusa e opaca com a absortividade espectral e a irradiação apresentadas a seguir:Qual é a absortividade total da superfície para a irradiação especificada? Se a superfíc
47 - O aço laminado que emerge da seção de laminação a quente de uma usina siderúrgica tem uma temperatura de 1200K , uma espessura δ = 3m m e a seguinte distribuição para a emissividade hemisférica e
55 - Um pequeno disco com 5 mm de diâmetro está posicionado no centro de uma cúpula hemisférica isotérmica. O disco é difuso e cinza com uma emissividade de 0,7 e é mantido a 900K . A cúpula hemisféri