Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 37

Uma superfície opaca e difusa, a 680   K , tem emissividades espectrais ε λ = 0 para 0 ≤ λ ≤ 3   μ m ; ε λ = 0 , 4 para 3 < λ ≤ 10   μ m ; e ε λ = 0 , 7 para 10 < λ < ∞ . Um fluxo radiante de 1000   W / m 2 , uniformemente distribuído entre 1 e 6   μ m , incide sobre a superfície com um ângulo de 30 ° em relação à sua normal.

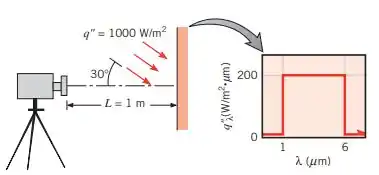
Calcule a potência radiante total que sai de uma área da superfície com 10 – 4   m 2 e atinge um detector de radiação que está posicionado ao longo da direção normal à essa área. A abertura do detector tem 10 - 5   m 2 e a sua distância da superfície é de   1   m .

Passo 1

E aí galera, beleza?

Vamos resolver essa questão juntos!

Começamos o nosso problema sabendo que a energia recebida pelo detector depende da emissão e reflexão do alvo:

q d = I e + A s cos ⁡ θ d - s ∆ ω d - s

Abrindo essa equação:

q d = ε σ T s 4 + ρ G π A s A d L 2

Isolando a emissividade:

ε = ∫ 0 ∞ ε λ E λ b 680   K d λ E b   680   K = ε 1 F 3 → 10   μ m + ε 2 F 10 → ∞

Pela Tabela 12.2, obtemos:

λ T = 2040   μ m ⋅ K e F 0 → 3   μ m = 0,073

λ T = 6800   μ m ⋅ K e F 0 → 3   μ m = 0,796

Substituindo os dados:

ε = 0,4 ⋅ 0,796 - 0,073 + 0,7 ⋅ 1 - 0,796 = 0,432

Passo 2

Desse modo:

ρ = ∫ 0 ∞ ρ λ G λ d λ G = ∫ 0 ∞ 1 - ε λ q λ ' ' d λ q ' ' = 1 - ε 1 ⋅ F 1 → 3 μ m + 1 - ε 2 ⋅ F 3 → 6   μ m

ρ = 1 - 0 ⋅ 0,073 - 0 + 1 - 0,4 ⋅ 0,50 - 0,073 = 0,33

Por fim, calculando a potência radiante total:

q d = ε σ T s 4 + ρ G π A s A d L 2

Com:

G = q ' ' ⋅ cos ⁡ θ 1 = 1000 ⋅ cos ⁡ 30 ° = 866   W / m 2

Temos:

q d = 0,432 ⋅ 5,67 × 10 - 8 ⋅ 680 4 + 0,33 ⋅ 866 π ⋅ 10 - 4 ⋅ 10 - 5 1 2

q d = 1,76 × 10 - 6   W

E assim a gente finaliza a nossa questão!

Resposta

q d = 1,76 × 10 - 6   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

53 - Seja o Problema 4.51.(a) Os estudantes receberam, cada um, um espelho de prata, plano e de primeira superfície, com os quais, coletivamente, irradiam o navio de madeira no local B. A reflexão no
56 - A absortividade hemisférica espectral de uma superfície opaca tem o comportamento mostrado a seguir.Qual é a absortividade solar, α S ? Se for considerado que ε λ = α λ e que a superfície se enco
44 - Estime a emissividade hemisférica total ε de aço inoxidável polido a 800K , usando a Equação 12.43 com as informações fornecidas na Figura 12.17. Suponha que a emissividade hemisférica é igual à
51 - A distribuição da refletividade espectral de uma tinta branca (Figura 12.22) pode ser aproximada pela seguinte função degrau:Uma pequena placa plana revestida com essa tinta encontra-se suspensa
46 - Para um comprimento de onda λ especificado, medidas da intensidade espectral I λ , e ( λ ,T )=ε λ I λ , c n da radiação emitida por uma superfície difusa podem ser usadas para determinar a temper