Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 50

Uma amostra muito pequena de uma superfície opaca encontra-se inicialmente a 1200   K e tem a absortividade hemisférica espectral mostrada na figura.

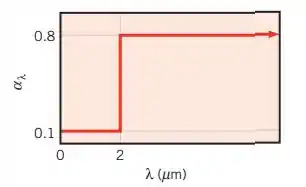
A amostra é colocada no interior de um grande compartimento cujas paredes têm uma emissividade de 0,2 e são mantidas a 2400   K .

(a) Qual é a absortividade hemisférica total da superfície da amostra?

(b) Qual é sua emissividade hemisférica total?

(c) Quais são os valores da absortividade e da emissividade após a amostra permanecer no interior do compartimento por um longo período de tempo?

Passo 1

Letra a)

Começamos o nosso problema sabendo que a absortividade hemisférica total segue a seguinte relação:

G λ = E λ , b T v i z

Ou seja, a irradiação corresponde ao poder emissivo espectral de um corpo negro no recinto temperatura e é independente da emissividade do compartimento.

α = ∫ 0 ∞ α λ G λ d λ ∫ 0 ∞ G λ d λ = ∫ 0 ∞ α λ E λ , b λ , T v i z d λ E b T v i z

α = α 1 ∫ 0 2   μ m E λ , b λ , T v i z d λ σ T v i z 4 + α 2 ∫ 2   μ m ∞ E λ , b λ , T v i z d λ σ T v i z 4

α = α 1 F 0 → 2   μ m + α 2 1 - F 0 → 2   μ m

Pela Tabela 12.2, para λ T = 2 ⋅ 2400 = 4800   μ m ⋅ K , temos:

F 0 → 2   μ m = 0,6076

Assim:

α = 0,1 ⋅ 0,6076 + 0,8 ⋅ 1 - 0,6076

α = 0,6076

Passo 2

Letra b)

A emissividade hemisférica total segue a seguinte equação:

ε = ∫ 0 ∞ ε λ E λ , b λ , T s d λ ∫ 0 ∞ E λ , b λ , T s d λ

Sendo:

ε λ = α λ

Temos:

ε = α 1 ∫ 0 2   μ m E λ , b λ , T s d λ σ T s 4 + α 2 ∫ 2   μ m ∞ E λ , b λ , T s d λ σ T s 4

ε = α 1 F 0 → 2   μ m + α 2 1 - F 0 → 2   μ m

Pela Tabela 12.2, para λ T = 2 ⋅ 12 00 = 2400   μ m ⋅ K , temos:

F 0 → 2   μ m = 0,1403

Assim:

ε = 0,1 ⋅ 0 , 1403 + 0,8 ⋅ 1 - 0,1403

ε = 0 , 702

Passo 3

Letra c)

Após um longo período de tempo, a superfície estará na temperatura do compartimento.

Esta condição de equilíbrio térmico é descrita pela Lei de Kirchoff, a qual diz que:

ε = α = 0,375

Até a próxima questão!

Resposta

a )   α = 0,6076

b )   ε = 0,702

c )   ε = α = 0,375

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A emissividade direcional total de materiais não metálicos pode ser aproximada por εθ = εn cos(θ), sendo εn a emissividade normal. Mostre que a emissividade hemisférica total de tais materiais é 2/3 d
Para os materiais A e B, cujas emissividades hemisféricas espectrais variam com o comprimento de onda conforme mostrado a seguir, como a emissividade hemisférica total varia com a temperatura? Expliqu
Um pequeno objeto metálico, inicialmente a Ti = 1000 K, é resfriado por radiação em uma câmara de vácuo a baixa temperatura. Uma das duas finas camadas de revestimento pode ser aplicada no objeto. As
Uma esfera encontra-se suspensa no ar de um quarto escuro e é mantida a uma temperatura uniforme que a mantém incandescente. Quando vista, pela primeira vez a olho nu, a esfera parece estar mais brilh
Considere a superfície direcionalmente seletiva que tem a emissividade direcional εθ mostrada a seguir.Supondo que a superfície seja isotrópica na direção ϕ, calcule a razão entre a emissividade norma