Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Diferença de Potencial

Ver Todos os Exercícios

Teoria

A diferença de potencial, também chamada de tensão ou para os íntimos d.d.p, é o trabalho necessário para que uma carga elétrica se desloque de um ponto A para um ponto B, dentro de um circuito elétrico fechado.

Fórmula da Diferença de Potencial - Lei de Ohm

A lei de Ohm diz que a corrente elétrica que percorre um circuito elétrico fechado é diretamente proporcional a diferença de potencial (ddp) aplicada no mesmo.

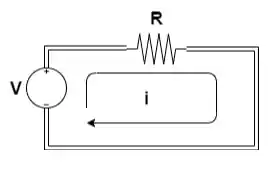
Circuito elétrico.
Circuito elétrico.

Ou seja, se aplicarmos uma diferença de potencial em dois terminais, fechando um circuito elétrico, a corrente gerada vai ser proporcional a essa ddp. Isso é, quanto maior a diferença de potencial, maior é a corrente que irá circular nesse circuito.

A fórmula da diferença de potencial tem essa carinha aqui:

Onde:

  • é a diferença de potencial aplicada, também chamada de tensão e é medida em volts ;
  • é a corrente que foi gerada, medida em ampère ;
  • é a proporção entre a corrente e a tensão, ou seja, a resistência que o corpo oferece à passagem de corrente. Medida em ohms .

Diferença de Potencial entre Dois Pontos

A lei de Ohm nos permite calcular a diferença de potencial em um circuito, mas, e se quisermos calcular a diferença de potencial entre dois pontos?!

Vamos considerar o seguinte circuito elétrico real:

Circuito Elétrico Real
Circuito Elétrico Real

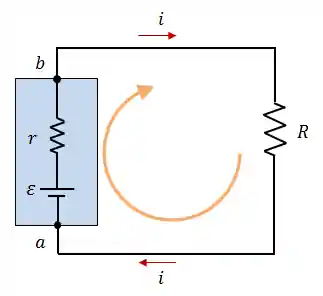
Na figura acima temos um circuito elétrico, composto por uma resistência , uma corrente e uma fonte real com uma resistência interna .

Como Calcular a Diferença de Potencial entre Dois Pontos

-Beleza, mas como vamos calcular a diferença de potencial entre os pontos e ?

Excelente pergunta! Para isso vamos relembrar a Lei das Malhas de Kirchoff:

A lei das malhas diz que para a soma dos potenciais elétricos ao longo de uma malha fechada é igual a zero. Matematicamente podemos escrever assim:

Ou seja, se somarmos o potencial elétrico no ponto inicial com todas as variações de potencial ao longo do percurso que escolhemos, o resultado deve ser igual ao potencial no ponto final . Assim:

Isolando o potencial elétrico nos pontos e , ficamos com:

Mas, a corrente do circuito, quando percorremos a malha inteira, é:

Substituindo, na fórmula da diferença de potencial, temos:

Agora organizamos a expressão e finalmente conseguimos calcular a diferença de potencial entre os pontos e :

Agora, vamos praticar com exercícios?!

Diferença de Potencial entre Dois Pontos

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 189-5. Modificada.

Uma bateria de automóvel com uma força eletromotriz de 12 V e uma resistência interna de 0,040 Ω está sendo carregada com uma corrente de 50 A . Determine

  1. a diferença de potencial V entre os terminais da bateria;
  2. a potência P i dissipada no interior da bateria;
  3. a potência P f e m fornecida pela bateria

Passo 1

a)

Se uma bateria está sendo carregada, ela está recebendo energia. Teríamos mais ou menos algo do tipo.

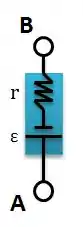
Passo 2

Como ele está carregando teremos um aumento do potencial dentro da bateria, logo V > 0 .

Logo, teremos que:

V A B = ε - r i = 12 - 0,04 ⋅ 50 = 10   V

Passo 3

b)

A potência vai ser dissipada pela resistência interna, ou seja, ele perguntou qual a potência dissipada pela resistência interna. Dada aqui por:

P = r i 2 = 0,04 ⋅ 50 2 = 100 W

Passo 4

c)

Nada mais nada menos é a potência do gerador, que pode ser calculada por:

P = i ⋅ ε = 12 ⋅ 50 = 600 W

E é isso aí, pessoal! :D

Resposta

  1. V A B = 10 V
  2. 100 W
  3. 600 W

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 190-13. Modificada.

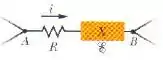
Na figura abaixo o trecho A B do circuito dissipa uma potência de 50 W quando a corrente i = 1 A tem o sentido indicado. O valor da resistência R é 2 Ω .

  1. Qual é a diferença de potencial entre A e B ?

    2. O dispositivo X não tem resistência interna.

  2. Qual é a força eletromotriz do dispositivo X?

Passo 1

a)

Temos dois dispositivos ligados, um resistor e X.

Independentemente do que está ligado ali, o potencial entre A e B será sempre P = V . I , sendo V a soma dos potenciais de R e de X .

V A B = V X + V R

Mas pera, para tudo! Nesse item A ele nos dá a potência e nos dá a corrente, logo a gente já tem V . :D

P A B = V A B . I

V A B = P A B I = 50 1 = 50 V

Passo 2

b)

Estamos seguros pelo enunciado que o dispositivo R e X estão dissipando potência, logo os sinais da diferença de potencial serão iguais.

Se ele nos diz que X não tem resistência interna, V x = ε x . Desta forma poderemos calcular, pela formulinha lá do passo 1.

V A B = V X + V R = ε x + R i

ε x = V A B - R i = 50 - 2.1 = 48 V

Resposta

  1. V A B = 50 V
  2. ε x = 48 V

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 190-18. Modificada

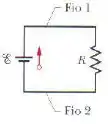
A figura abaixo mostra um resistor de resistência R = 6,00 Ω ligado a uma fonte ideal de força eletromotriz ε = 12 V através de dois fios de cobre. Cada fio tem 20 c m de comprimento e 1 m m de raio. Até então sempre desprezamos a resistência dos fios de ligação. Verifique se a aproximação é válida para o circuito da imagem, determinando:

  1. a diferença de potencial entre as extremidades do resistor;
  2. a diferença de potencial entre as extremidades de um dos fios.
  3. a potência dissipada em um dos fios;

Dados:

ρ c o b r e = 1,69.10 - 8 Ω . m

Passo 1

a)

Bem, temos que demonstrar nessa questão o porquê de podermos desprezar a resistência nos fios. Então vamos à caça dessa demonstração respondendo as alternativas.

Considerando a resistência de cada fio de cobre, e concentrando-as em dois lugares,a gente vai ter algo mais ou menos assim:

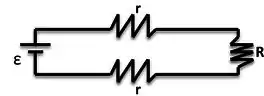
Passo 2

Aplicando a Lei das Malhas de Kirchhoff com uma corrente no sentido horário, teremos:

ε - r i - R i - r i = 0

i = ε 2 r + R = 12 2 r + 6

Passo 3

Mas como que calcula o r ? Você se lembra? Eu sim, haha!

Pela Lei de Ohm a gente tinha lá a seguinte relação:

r = ρ L A

Como o fio é circular, o A = π R a i o 2 .

r = ρ L π R a i o ² = 1,69.10 - 8 . 0,2 π . 10 - 6 = 0,0011 Ω

Logo, a corrente vai ser:

i = 12 0,0022 + 6 = 1,9993 A

Passo 4

Agora sim, achando a diferença de potencial nas extremidades do resistor, basta fazer

V = R i = 6.1,993 = 11,996 V ≈ 12 V

Viu como fica próximo de 12V? Só assim já provamos que é quase desprezível ter ou não ter considerado a resistência de cada fio.

Mas vamos lá seguindo na questão!

Passo 5

b)

Basta fazer a mesma coisa que fizemos no passo anterior só que pra resistência menor.

Bora lá!

V = r . i = 0,0011.1,993 = 2,15.10 - 3 V

Ou seja, eles tiram uma voltagem super mini do circuito. Desconsiderar r seria bem ok. :}

Passo 6

A potência dissipada em um fio de cobre, será dada por:

P = r i ² = 4,3.10 - 3 W

Também super mini potência.

Moral da história? Pra fios pequenos, como esse, de apenas 20 c m vale a pena desprezar a resistência.

Mas isso sempre é válido? Não! Por exemplo o fio que liga a hidrelétrica até a sua casa são milhares de kilômetros de distância e a energia dissipada seria beeeem maior!

Resposta

  1. V R = 11,996 V
  2. V r = 2,15 m V
  3. P r = 4,3 m W

Exercício Resolvido #4

Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 25.68, pp. 165.

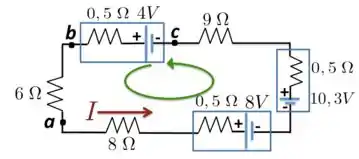
Dada a Figura abaixo,

  1. Qual é a diferença de potencial V a d ?

  2. Qual é a voltagem nos terminais da bateria de 4,0   V ?

  3. Uma bateria com fem igual a 10,30   V e resistência interna 0,50   Ω é inserida no circuito no ponto d , com seu terminal negativo conectado ao terminal negativo da bateria de 8,0   V . Qual é agora a diferença de potencial V b c nos terminais da bateria de 4,0   V ?

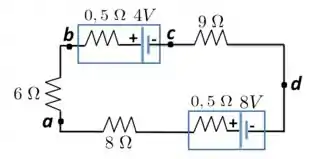
Passo 1

a) Para encontrar a diferença de potencial V a d entre os pontos a e d , temos que encontrar primeiro qual o valor da corrente que circula no circuito. Para isso, vamos considerar a Figura abaixo, em que desenhamos a corrente I no sentido anti-horário, que também é o sentido que escolhemos para a malha.

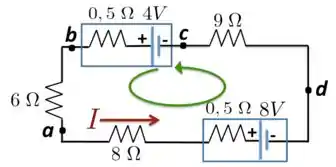
Partindo do ponto a e voltando para ele percorrendo a malha no sentido anti-horário, temos que

- 8 I - 0,5 I - 8 - 9 I + 4 - 0,5 I - 6 I = 0 ⇒ - 24 I = 4   .

Com isso, chegamos a

I = - 1 6   A   .

Isso significa que escolhemos o sentido da corrente errado. Ou seja, a corrente na Figura acima está no sentido horário, porém seu módulo é I = 1 6   A   .

Agora, tomando o sentido horário para a corrente, vamos tomar apenas o trecho que vai do ponto a até o ponto d

V a + 1 6 × 8 + 1 6 × 0,5 - 8 = V d ⇒ V a - V d ≡ V a d = 79 12   V ≈ 6,58   V .

Passo 2

b) Indo de b para o ponto c , que é o sentido correto para a corrente I , temos

V b - 1 6 × 0,5 - 4 = V c ⇒ V b - V c ≡ V b c = 49 12   V ≈ 4,08   V   .

Passo 3

c) Com a nova bateria, precisamos calcular novamente o valor da corrente no circuito. Para isso, vamos utilizar o mesmo sentido anti-horário para a malha e para a corrente.

Partindo do ponto a e retornando a ele, temos

- 8 I - 0,5 I - 8 + 10,3 - 0,5 I - 9 I + 4 - 0,5 I - 6 I = 0   .

Resolvendo essa equação, temos

I = 0,257   A   .

Portanto, para sabermos a diferença de potencial entre os pontos b e c , podemos tomar o sentido nesse trecho indo de c para b

V c + 4 - 0,5 × 0,257 = V b   ⇒ V b - V c ≡ V b c = 3,87   V   .

Resposta

  1. V a d = 79 12   V ≈ 6,58   V   ;

  2. V b c = 49 12   V ≈ 4,08   V   ;

  3. V b c ≈ 3,87   V   .

Exercício Resolvido #5

Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 25.53, Adaptado, pp. 163.

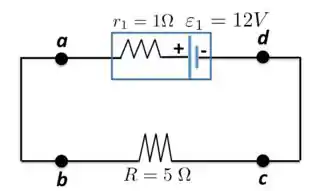
No circuito indicado na Figura abaixo, calcule:

  1. a taxa de conversão de energia interna (química) em energia elétrica no interior da bateria;

  2. a taxa de dissipação da energia elétrica na bateria;

  3. a taxa da dissipação a energia elétrica na resistência externa;

  4. a ddp entre os pontos a e d do circuito;

  5. a ddp entre a e c e entre os pontos b e c .

Passo 1

a) Para sabermos qual é a taxa com a qual a bateria transforma energia química em energia elétrica, precisamos saber qual o valor da corrente I que circula no circuito. Para isso, vamos considerar o sentido anti-horário da malha e da corrente indicados na Figura abaixo.

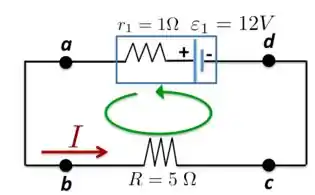
Saindo do ponto b e percorrendo a malha até voltarmos para esse ponto, temos, pela lei das malhas, que

- 5 I + 12 - I = 0 ⇒ I = 2   A .

Portanto, a taxa de conversão de energia química em energia elétrica é

P = ε 1 I = 24   W   .

Passo 2

b) Como a bateria tem resistência interna, quando a corrente passa pela bateria, parte da energia é dissipada por r 1 e essa taxa é de

P = r 1 I 2 = 1 × 2 2 = 4   W   .

Passo 3

c) A taxa de dissipação de energia no resistor externo R é de

P = R I 2 = 5 × 2 2 = 20   W   .

Passo 4

d) Considerando apenas o trecho que vai do ponto d até o ponto a da Figura acima, temos o seguinte

V d + ε 1 - r 1 I = V a ⇒ V d - V a ≡ V a d = r 1 I - ε 1   .

Substituindo os valores dados non enunciado, temos

V a d = - 10   V   .

Passo 5

e) Como entre os pontos a e b não há nenhuma queda de potencial, a diferença de potencial V a c = V b c ≡ V . Portanto, o valor para essas duas ddp’s é de

V a - V c = V b - V c ≡ V = R I = 10   V   .

Resposta

  1. P = 24   W   ;

  2. P = 4   W   ;
  3. P = 20   W   ;

  4. V a d = - 10   V   ;

  5. V = 10   V   .

Exercício Resolvido #6

Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 26.5, pp. 193.

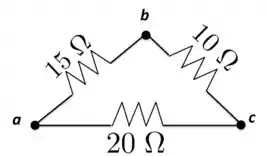
Uma combinação triangular de resistores é indicada na Figura abaixo. Qual é a corrente que essa combinação consumirá de uma bateria de 35,0   V , com resistência interna desprezível, quando ela é conectada através dos pontos :

  1. a b ;
  2. b c   ;
  3. a c   ;

Passo 1

a) Quando a bateria é conectada entre os pontos a e b , temos o resistores de 10   Ω e de 20   Ω em série e o resultado dessa associação em paralelo com o resistor de 15   Ω .

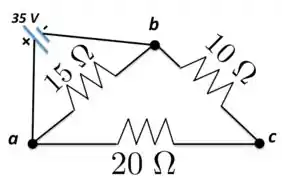
Então, a primeira coisa que precisamos calcular aqui é a resistência equivalente desse circuito. Nesse caso, o resistor R 1 resultado da associação entre os resistores 10   Ω e o de 20   Ω é

R 1 = 10 + 20 = 30   Ω   .

Esse resistor R 1 está em paralelo com o de 15   Ω . Por isso, teremos o seguinte:

1 R e q = 1 R 1 + 1 15 = 1 30 + 1 15   ⇒ R e q = 30 × 15 30 + 15 = 10   Ω   .

Portanto, a corrente do circuito nesse caso é

I = 35 R e q = 3,5   A   .

Passo 2

b) Agora, neste caso, o resistor de 10   Ω é que estará em paralelo com o resultado da associação em série dos resistores de 15   Ω e de 20   Ω . O valor dessa associação em série é R 1 = 35   Ω .

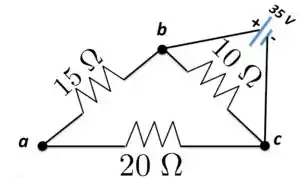
Portanto, a associação em paralelo terá resistência equivalente a

R e q = R 1 × 10 R e q + 10   = 35 × 10 35 + 10 = 7,78   Ω   .

A corrente é, então,

I = 35 7,78 ≈ 4,5   A   .

Passo 3

c) Aqui, de maneira semelhante a dos casos anteriores, os resistores de 15   Ω e o de 10   Ω estão em série e tem resistência equivalente dada por R 1 = 25   Ω .

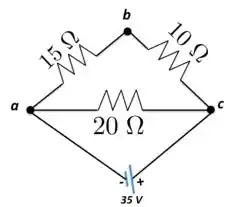
A resistência equivalente do circuito todo será

R e q = 25 × 20 25 + 20 = 11,1   Ω   .

Então, a corrente será

I = 35 R e q = 35 11,1 = 3,15   A   .

Resposta

  1. I = 3,5   A   ;

  2. I = 4,5   A   ;

  3. I = 3,15   A   .

Exercícios de Livros Relacionados

Suponha que, enquanto você está sentado em uma cadeira, a separação de cargas entre sua roupa e a cadeira faça com que seu corpo fique a um potencial de 200 V, com uma capacitância de 150 pF entre voc
A Fig. 27-30 mostra um resistor de resistência R = 6,00 Ω ligado a uma fonte ideal de força eletromotriz ε = 12,0 V através de dois fios de cobre. Cada fio tem 20,0 cm de comprimento e 1,00 mm de raio
(a) Na Fig. 27-28, qual deve ser o valor de R para que a corrente no circuito seja 1,0 mA? Sabe-se que ε 1 = 2,0 V , ε 2 = 3,0 V ,r 1 = r 2 = 3,0 Ω . (b) Qual é a potência dissipada em R ?
Um gráfico da corrente como função da tensão para um diodo Esaki é mostrado na Figura 25-81.a) Faça um gráfico da resistência diferencial do diodo como função da tensão. A resistência diferencial R d
(b) Se 3,40 × 10 18 elétrons passam pela fonte por segundo, qual é a potência da fonte em watts?