Circuito de uma Malha
Produzido por Bruno SoaresTeoria
Para entender como resolver questões envolvendo circuitos, nós precisamos entender as regras que envolvem esse tipo de problema.
Essas regras são muito importantes, e você precisa me prometer que vai guardá-las contigo pelo resto da vida.
Sempre que formos trabalhar com circuitos precisamos escolher um sentido para percorrer uma determinada malha. Se o sentido que escolhermos é o mesmo sentido, ou o sentido oposto da corrente, isso vai mudar na forma como avaliaremos a diferença de potencial através de cada componente.
Neste capítulo, as setas laranjas indicarão o sentido em que estamos percorrendo uma determinada malha, ou atravessando determinado componente do circuito.
Regra das Resistências
- Quando atravessamos uma resistência no sentido da corrente, a diferença de potencial é ;
- Quando atravessamos uma resistência no sentido oposto ao da corrente, a diferença de potencial é ;
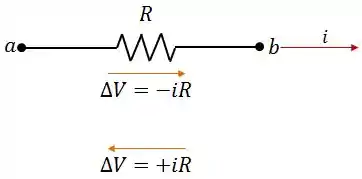
Regra das Fontes
- Quando atravessamos uma fonte do terminal negativo (barra menor) para o positivo (barra maior), a diferença de potencial é ;
- Quando atravessamos uma fonte do terminal positivo para o negativo, a diferença de potencial é ;
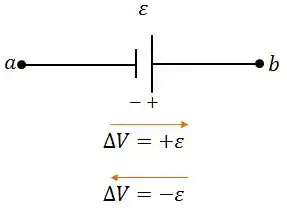
Regra das Malhas (Lei das malhas de Kirchhoff)
- A soma de todas as diferenças de potencial quando você percorre uma malha é igual a zero.
Vamos aplicar a Regra das Malhas a um circuito simples:
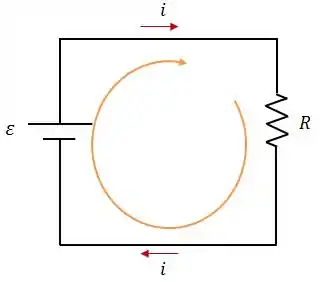
Repare que, neste sentido, estamos atravessando a fonte do negativo para o positivo, então a diferença de potencial ali será . Além disso, atravessamos a resistência no mesmo sentido da corrente, logo, a diferença de potencial ali será .
Portanto, aplicando a Lei das malhas de Kirchhoff, teremos:
Além disso, podemos ver que, em um circuito simples com uma fonte ideal e um resistor, a força eletromotriz será:
Fontes com Resistência Interna (Fontes Reais)
A resistência interna da fonte é a resistência elétrica dos materiais condutores que existem no interior da fonte e, portanto, é parte integrante da fonte.
Para entender o que acontece em um circuito com fontes reais, vamos analisar um circuito simples composto por uma fonte real e um resistor:
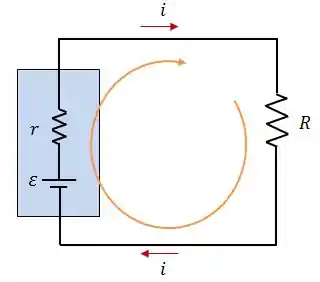
Aplicando a Lei das malhas de Kirchhoff, teremos:
A partir disso, podemos ver que a corrente elétrica no circuito será dada por:
Se quiséssemos trabalhar com o caso da fonte ideal, bastaria dizer que (ou seja, a fonte não possui resistência interna).
Agora, vamos exercitar!
Regra das Resistências
Regra das Fontes
Regra das Malhas (Lei das malhas de Kirchhoff)
Fontes com Resistência Interna (Fontes Reais)
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 189-7.
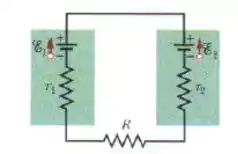
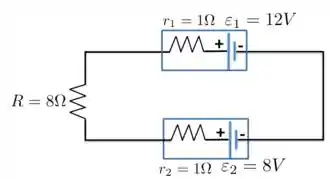
Na figura abaixo as fontes ideais têm forças eletromotrizes e e os resistores têm resistências Determine:
- a corrente do circuito;
- a potência dissipada no resistor ;
- a potência dissipada no resistor ;
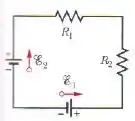
Passo 1
Então, pessoal! Temos uma malha simples. Vamos devagar, aprendendo a cada passo.
Ele nos forneceu o valor das duas fontes e dos resistores e está pedindo pra a gente calcular primeiramente a corrente nesse circuito.
Como fazer? Vamos lá!
Passo 2
a)
Só relembrando as regrinhas:
Resistência
- Quando atravessamos uma resistência no sentido da corrente, a diferença de potencial é ;
- Quando atravessamos uma resistência no sentido oposto ao da corrente, a diferença de potencial é ;
Fonte
- Quando atravessamos uma fonte do terminal negativo (barra menor) para o positivo (barra maior), a diferença de potencial é ;
- Quando atravessamos uma fonte do terminal positivo para o negativo, a diferença de potencial é ;
Passo 3
Pela Lei das Malhas de Kirchhoff, a soma das ddp’s nesse circuito tem que ser zero.
Mas, nesse caso nós temos duas forças eletromotrizes, como vamos saber o sentido da corrente? Relaxa, nós podemos supor um sentido para a corrente. Supondo que esse seja o sentido horário, logo, teremos que:
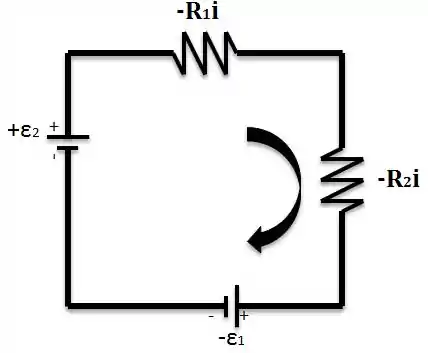
Isolando o teremos:
Como achamos um valor negativo para a corrente, podemos afirmar que supomos o sentido errado! Analisando o circuito podemos visualizar isso, afinal o sentido da corrente vai ser definido pela fonte de maior potencial no caso , ou seja o sentido da fonte é anti-horário.
Passo 4
b)
Aqui é só relembrar a formulinha de potência. Como aqui temos resistência e também a corrente é só usar:
Passo 5
c)
Mesma coisa da letra b, só trocando os valores.
E é isso aê!
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 190-19.
A corrente em um circuito com uma única malha e uma resistência é . Quando uma resistência de é ligada em série com , a corrente diminui para . Qual é o valor de
Passo 1
Parando pra refletir um pouco sobre essa questão. No primeiro caso temos o circuito de uma malha com apenas um resistor. Se tem um resistor, pra haver corrente tem que ter também uma fonte.
Então o primeiro circuito vai assim.
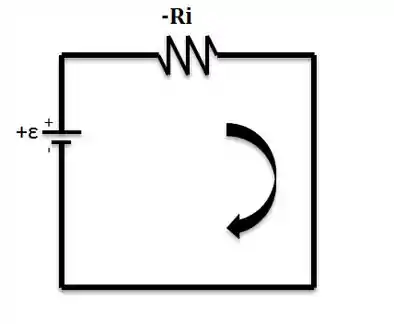
Bem simples, né?
Usando a Lei das Malhas, teremos:
Passo 2
Adicionando mais um resistor, só vamos acrescentar um termo aí na Lei das Malhas de . Assim, vai ficar:
Passo 3
Igualando com a equação da primeira, vamos ter que:
Substituindo os valores, vai ficar:
Resposta
Exercício Resolvido #3
UERJ- Lista de Exercícios- Circuitos Elétricos
Qual é a resistência interna da bateria na figura e que valor de potência é dissipado internamente na mesma?
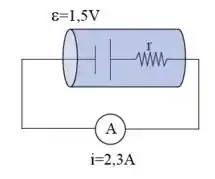
Passo 1
Para determinar a resistência interna da bateria, basta usar a regra das malhas para o circuito, teremos então:
Como e , temos:
Passo 2
Para determinar a potência dissipada, temos a seguinte relação:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 189-12.
- Na figura abaixo qual deve ser o valor de para que a corrente no circuito seja ?
Sabe-se que , , .
- Qual é a potência dissipada em
Passo 1
a)
Ele nos dá as informações dos dois geradores e das suas resistências internas e ainda nos dá a corrente . Só o que sobra pra a gente é que? O resistor . Vai sair bem rápido usando Lei das Malhas. Saca só!
Passo 2
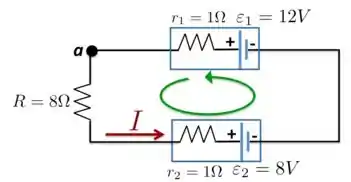
Vamos supor esse sentido indicado para a corrente e uma malha sentido horário.
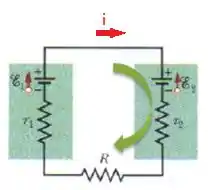
Usando o mesmo sentido (horário) para a Lei das Malhas do nosso amigo Kirchhoff, teremos:
Isolando o , teremos:
Como encontramos um valor negativo para , erramos no sentido da corrente!
Mas, calma! Fazendo de novo, agora para uma corrente no sentido anti-horário. Usando o sentido anti-horário também para a Lei das Malhas, obtemos:
Agora sim!
Passo 3
b)
Lembra como calcula a potência somente?
Primeiro temos que ver o que a gente tem. Nesse caso, temos a resistência que a gente acabou de achar e também a corrente.
Calculando a potência com esses dados é só usar:
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 196-74.
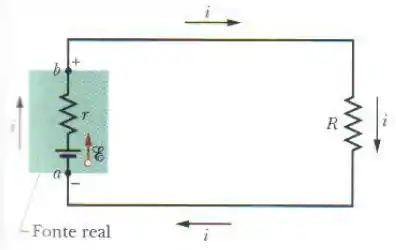
Na figura abaixo mostre que a potência dissipada em é máxima para . Mostre que essa potência máxima é .
Passo 1
Opa! Primeiro de tudo, é bom ter uma noção quais as variáveis nós precisamos lidar para poder resolver esse problema. Ele fala em potência e a gente já vê na figura as grandezas e .
Pra calcular a potência no resistor com esses dados é só usar
Passo 2
Mas a gente não sabe quem é , então vamos busca-la!
Pela Lei das Malhas, adotando o sentido da corrente, teremos:
Show?
Show!
Passo 3
Agora é só tacar lá na fórmulinha da potência.
Passo 4
Mas pera, agora vamos entrar no mais delicado da questão.
Vemos que pra uma dada fonte com ddp e , para cada valor pra teremos um valor pra . Assim, podemos dizer que é uma função de e pra otimizar essa função temos que derivar e igualar a zero. Lembra lá do cálculo? Espero que sim. :}
Derivando, pela regra do quociente, vamos ter:
Fazendo o MMC disso aí, vamos ter:
Passo 5
Agora é só substituir o valor de lá na potência. Daí, teremos:
Como queríamos demonstrar!!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 25.35, pp. 162.
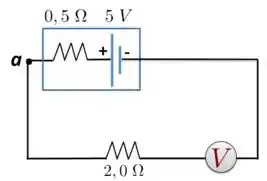
Um voltímetro ideal está conectado a um resistor de e a uma bacteria com fem igual a e uma resistência interna de , como indicado na Figura abaixo.
- Qual é a corrente no resistor de ?
- Qual é a voltagem entre os terminais da bateria durante a passagem da corrente?
- Qual é a leitura do voltímetro? Explique suas respostas.
Passo 1
a) Como temos um voltímetro ideal, a resistência que ele possui é infinita. Por isso, não passa nenhuma corrente pelo circuito, já que ele está ligado em série com a bateria e com o resistor de .
Passo 2
b) A voltagem da bateria seria menor durante a passagem de alguma corrente, pois ela tem uma resistência interna de No entanto, como neste caso não temos corrente passando pelo circuito, a voltagem da bateria é
Passo 3
c) Como não passa nenhuma corrente pelo circuito, o voltímetro mostra o mesmo valor que a bateria, ou seja, de .
Resposta
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 25.52, pp. 163.
Um voltímetro ideal está conectado aos terminais de uma bateria de , e um aparelho eletrodoméstico de também está conectado a esses terminais. Se a leitura do voltímetro for de ,
- quanto potência está sendo dissipada pelo aparelho e
- qual é a resistência interna da bateria?
Passo 1
a) Esse é um caso de um circuito em que temos um resistor ligado em série com uma bateria que possui resistência interna . Portanto, temos um circuito de apenas uma malha.
Como a leitura do voltímetro, que está em paralelo com a bateria, é de , os terminais do resistor de estão ligados a essa diferença de potencial. Então, a potência dissipada no resistor do eletrodoméstico é de
Passo 2
b) Se o voltímetro mede uma ddp de , então, é uma queda de potencial devida à resistência interna da bateria. Agora, precisamos saber qual é a corrente que passa pela bateria para calcularmos essa resistência.
A corrente que passa pelo circuito e que atravessa a bateria é
Portanto, a resistência interna da bateria é
Resposta
Exercício Resolvido #8
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 25.79, pp. 166.
No circuito da Figura abaixo, calcule:
- a corrente através do resistor de ;
- A taxa total da dissipação de energia elétrica no resistor de e nas demais resistências internas das baterias;
- Em uma das baterias ocorre conversão de energia química em elétrica. Em qual das duas baterias isso está ocorrendo e qual é a taxa da conversão?
- Em uma das baterias ocorre conversão de energia elétrica em química. Em qual das baterias isso está ocorrendo e qual é a taxa da conversão?
- Mostre que a taxa global de produção da energia elétrica é igual à taxa global de dissipação da energia elétrica.
Passo 1
a) Para obtermos a energia dissipada total nas resistências do circuito, precisamos encontrar o valor da corrente . Para isso, vamos considerar o sentido da malha que está na Figura abaixo, partindo do ponto e percorrendo toda a malha no sentido anti-horário somando as quedas de potencial até voltarmos para ponto de novo.
Isso significa, fazendo as contas, que
Essa é a corrente que passa no resistor.
Passo 2
b) A taxa total de energia dissipada é a potência dissipada. Como estamos interessados na potência total, temos que fazer a seguinte conta
Colocando os valores dessas resistências e também o valor da corrente, que é , temos
Passo 3
c) Ocorre conversão de energia química em energia elétrica quando a corrente passa em uma bateria do pólo negativo para o pólo positivo, que é o caso da bateria de . Isso porque a bateria fornece uma energia química para que as partículas carregadas da corrente saiam de um potencial mais baixo, negativo, para um potencial mais alto no pólo positivo da bateria.
Em outras palavras, essa energia química é o trabalho que essa bateria realiza sobre as cargas para que elas entrem no pólo de menor potencial e cheguem ao de maior potencial. A taxa com a qual ocorre essa conversão é
Passo 4
d) No caso da bateria de , as cargas chegam no pólo positivo, de maior potencial, e saem pelo de menor potencial, o pólo negativo. Nessa situação, há uma conversão de energia elétrica em energia química dentro dessa bateria.
A taxa com a qual ocorre essa conversão é
Passo 5
e) A taxa dissipada é dada pela soma das taxas dissipadas em cada resistor mais o valor da taxa de conversão de energia elétrica em energia química, que é Portanto
que é exatamente o valor da energia total fornecida pela bateria de . Essa é a taxa total de perda de energia que se iguala à taxa total de produção de energia elétrica.