Teoria
Fala aí, você chegou no Responde Aí! E agora vamos te ensinar tudo sobre os materiais dielétricos
O que é um Dielétrico?
Um dielétrico nada mais é do que um isolante que pode ser polarizado por um campo elétrico externo.
Por exemplo, se você colocasse um condutor numa região de campo elétrico haveria indução de cargas até que fosse atingido o equilíbrio eletrostático. No dielétrico não é bem assim que acontece, pois ele é um isolante.
Como funciona um dielétrico?
O que ocorre é que os elétrons saem levemente de sua posição de equilíbrio e ocorre uma polarização (uma mini indução, digamos). Como é bem sabido, num material isolante pode haver campo mesmo no equilíbrio. Por conta dessa polarização, é criado um campo elétrico interno que diminui o campo que havia antes.
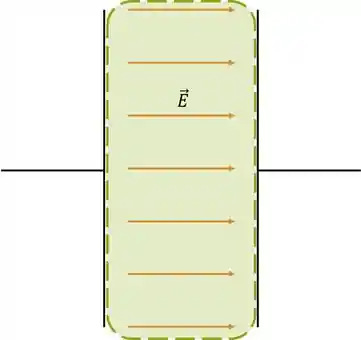
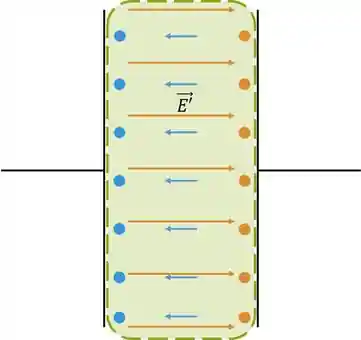
Por conta dessa diminuição do campo, o que ocorre é que o módulo da diferença de potencial diminui também.
Então se colocarmos um dielétrico entre as placas de um capacitor, temos que a voltagem diminui para uma mesma carga armazenada, e por consequência obtemos uma capacitância maior.
Constante Dielétrica de Alguns Materiais
A constante dielétrica
Dá só uma conferida na constante dielétrica de alguns materiais:

Pra saber mais sobre dielétricos, confere esse vídeo super maneiro que o Responde Aí preparou pra você 👇 🧡
Equações e Fórmulas dos Dielétricos
Como o dielétrico reduz a voltagem, podemos tirar deste fato uma série de conclusões!
Primeiramente vamos associar à ele a constante dielétrica, representada pela letra
Deste fato, podemos substituir na fórmula da capacitância e chegar em:
Ou seja, ao passo que a voltagem diminui, a capacitância aumenta. Além disso, por dividir a voltagem, podemos analisar a fórmula
Ou seja, reduz o campo também por um fator de
Ruptura dielétrica
Nós poderíamos meter um campo tão forte no dielétrico que nós induzíssemos as cargas nele como se fosse um condutor?
Sim. Se o campo for forte demais o dielétrico pode perder suas capacidades isolantes, pois você estaria fazendo algo muito mais forte que a polarização que nós comentamos. As cargas começariam à se mover de fato, certo? Então qual seria a diferença dele pra um condutor? Quase nenhuma! As cargas iam ser arrastadas pra superfície à força, ele iria ficando equipotencial, etc... Neste caso nós dizemos que ocorreu uma ruptura dielétrica.
Repare que aqui mantivemos a carga constante entre as placas do capacitor.
Capacitores dielétricos com DDP constante
A ideia é a seguinte. Temos inicialmente o nosso capacitor ligado a um circuito que é alimentado por uma ddp
Se liga! O capacitor vai continuar sendo alimentado pela ddp
Assim que colocamos o dielétrico, independente da situação, nós alteramos a capacitância do nosso capacitor que, nesse caso, passará a ser:
A carga no capacitor, assim como a capacitância, também irá aumentar:
No entanto a ddp permanece a mesma, bem como o campo elétrico entre as placas do capacitor:
Então fique de olho pra saber em qual situação estamos trabalhando, ou seja, carga constante ou ddp constante. Beleza?!
Agora vamos praticar com exercícios!