Exercícios de Dielétricos - Lista de Exercícios Resolvida

Duas placas paralelas possuem cargas iguais e opostas. Quando existe vácuo entre as placas, o módulo do campo elétrico é . Quando o espaço entre as placas é preenchido por um dielétrico, o campo elétrico possui módulo .

(a) Qual é o valor da constante dielétrica?

(b) Qual é a densidade de carga em cada superfície do dielétrico?

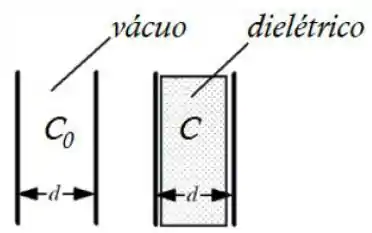
Um capacitor de placas paralelas é carregado com uma carga e, em seguida, a bateria é removida. Um pedaço de material de constante dielétrica é inserido entre as placas (vide figura).

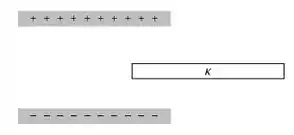
A carga armazenada no capacitor aumenta, diminui ou permanece a mesma? Explique.

Um capacitor tem armaduras paralelas cuja área é de e estão separadas por . Uma bateria carrega as armaduras até que a diferença de potencial entre elas seja , sendo então desligada. Uma placa de dielétrico de constante dielétrica , é então colocada entre as armaduras do capacitor. Qual a capacitância antes e após introduzirmos o dielétrico?

Considere um capacitor ideal de placas quadradas, planas e paralelas. Mantendo-se a carga de cada placa constante, uma chapa espessa de isolante, é inserida na região entre as placas do capacitor original. Sendo o módulo do campo elétrico entre as placas do capacitor original, e (i = 1, 2) os módulos do campo elétrico, nos pontos (i = 1, 2), após a introdução do

isolante, o que pode ser afirmado sobre tais módulos?

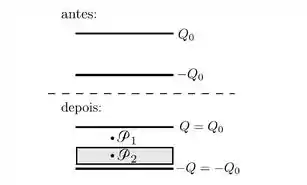
(a) .

(b)

(c) .

(d) .

(e) .

(f) .

(g) .

(h) .

Uma placa dielétrica de espessura e constante dielétrica é introduzida entre as placas de um capacitor plano, as quais estão separadas pela distância . Cada placa possui área igual a . Mostre que a capacitância é dada por:

Um capacitor com placas paralelas possui capacitância , quando existe ar entre as placas. A distância entre as placas é igual a .

(a) Qual é o módulo máximo de carga que pode ser colocado em cada placa, se o campo elétrico na região entre as placas não exceder ?

(b) Um dielétrico com é inserido entre as placas do capacitor, preenchendo completamente o volume entre elas. Qual passa a ser o módulo máximo de carga em cada placa, se o campo elétrico entre elas não exceder ?

Um capacitor de placas paralelas de área possui vácuo entre as placas, separadas por uma distância . Sua capacitância é .

Um outro capacitor tem placas de área separadas por uma distância , sendo que entre elas há um dielétrico de constante dielétrica . Sua capacitância vale . Determine a razão .

Das afirmativas abaixo, assinale a única que é incorreta.

1. O campo elétrico produzido por um corpo com carga total igual a zero pode ser diferente de zero;
2. O campo elétrico no interior de um material dielétrico é sempre zero, mesmo que ele esteja em uma região com campo elétrico;
3. O campo elétrico entre as placas de um capacitor isolado diminui quando a região entre suas placas é completamente preenchida por um material de constante dielétrica ;
4. Quando um material dielétrico é inserido entre as placas de um capacitor, surge uma densidade superficial de carga induzida nas superfícies do dielétrico que causa a mudança da capacitância;
5. Quando um material dielétrico é inserido entre as placas de um capacitor, é possível submeter esse capacitor à maiores diferenças de potencial, sem que ocorra a ruptura dielétrica.

Uma bola esférica, condutora, sólida, em equilíbrio eletrostático, de raio , possui carga total . Tal bola é circundada por uma coroa esférica, isolante (de constante dielétrica ), de raios interno e externo , com uma carga total , uniformemente distribuída (pelo interior da coroa).

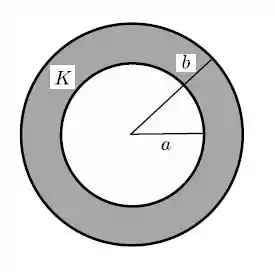
1. Calcule o vetor campo elétrico resultante (módulo, direção e sentido) nas três regiões: (I) ; (II) ; (III) .
2. Calcule o potencial elétrico resultante nas três regiões acima mencionadas, fazendo-o zero no infinito.

A figura abaixo ilustra um capacitor de placas metálicas esféricas de raios e , com . As placas são concêntricas e centradas na origem . O espaço entre as placas é completamente preenchido por uma substância não-condutora de constante dielétrica . Nas regiões restantes ( e ) há vácuo, onde é a distância radial até a origem . A constante de permissividade do vácuo é dada por .

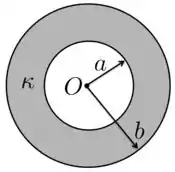
1. Calcule a capacitância do dispositivo usando a lei de Gauss, determinando a diferença de potencial entre as placas e finalmente aplicando a definição de capacitância.
2. Considerando que uma diferença de potencial é aplicada entre as duas placas metálicas, calcule a carga livre da placa interna.
3. Nas mesmas condições do item (b), calcule a carga ’ induzida na superfície do dielétrico que se encontra mais próxima da placa metálica interna.

Seja um capacitor ideal, com capacitância , de placas planas e paralelas, de mesma área e distância entre si, “recheado” com vácuo. Considere, agora, um novo capacitor , de placas planas e paralelas, “recheado” com um material isolante de constante dielétrica mas com distância entre as placas duas vezes maior que a do capacitor ; qual deve ser a nova área (das placas) para manter a capacitância original ? Considere, a seguir, um terceiro capacitor , de placas planas e paralelas, “recheado” com o mesmo material, mas agora com área (das placas) duas vezes maior que a do capacitor ; qual deve ser a nova distância entre as placas para manter a capacitância original ?

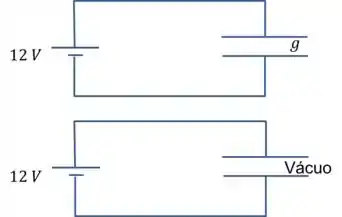
Dois capacitores de placas planas e paralelas idênticos são preenchidos com materiais dielétricos diferentes. O capacitor é preenchido com dielétrico de constante dielétrica e outro (capacitor ) com vácuo. Os capacitores são carregados com baterias idênticas de , como mostra a figura, que permanecem ligadas a eles. Assinale a afirmação incorreta:

a) A carga acumulada nas placas dos dois capacitores são diferentes

b) O campo elétrico no interior dos dois capacitores são iguais

c) A energia necessária para carregar os dois capacitores são iguais

d) A ddp entre as placas dos dois capacitores são iguais

e) A capacitância do capacitor A é maior que a do capacitor B

Um capacitor carregado tem um campo elétrico inicial e uma diferença de potencial inicial entre suas placas.

Sem desliga-lo da bateria que o carregou, uma placa de dielétrico é inserida e preenche completamente o volume entre as placas, que produz um campo elétrico e uma diferença de potencial entre elas.

O par de afirmações que melhor representa as relações entre os campos elétricos e as diferenças de potencial antes e depois da inserção do dielétrico é:

; ;

; ;

; ;

; ;

; ;

Um capacitor de placas paralelas, separadas por uma distância , é carregado a uma diferença de potencial por uma bateria.

Mantendo-se a bateria ligada, uma lâmina de material plástico de constante dielétrica é inserida entre as placas do capacitor, sem alterar as demais propriedades do sistema. A nova diferença de potencial entre as placas e o novo campo elétrico entre elas são, respectivamente:

e ;

e ;

e ;

e ;

Considere um capacitor esférico de raio interno e raio externo com uma carga , conforme mostra a figura abaixo.

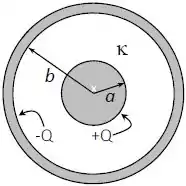
A região entre as placas do capacitor é preenchida por um dielétrico de constante dielétrica .

Use a Lei de Gauss em meios dielétricos para mostrar que o módulo do campo elétrico entre as placas do capacitor é

Calcule a capacitância deste capacitor.

Justificando claramente sua resposta, determine a carga induzida na superfície interna do dielétrico, ou seja, em .

Um capacitor possui placas paralelas separadas por uma distância igual a . O espaço entre as placas está cheio de poliéster (Constante dielétrica, ), que possui rigidez dielétrica . Qual a voltagem máxima, e a carga máxima possível que o capacitor pode suportar sem que ocorra ruptura dielétrica.

Considere que na ausência do poliéster o capacitor possui capacitância .

;

;

;

;

;

Um capacitor de placas paralelas é carregado por meio de uma bateria de corrente contínua até adquirir cargas e em cada uma de suas placas. Após o processo de carga, ele é desconectado da bateria e se insere entre suas placas um isolante de constante dielétrica que ocupa todo o espaço entre as placas. Nessas condições, qual das alternativas abaixo é incorreta

(a) A carga nas placas permanece a mesma

(b) O campo elétrico diminui de um fator de

(c) A diferença de potencial entre as placas diminui de um fator de

(d) A energia armazenada no capacitor diminui de um fator de

(e) A capacitância diminui de um fator de

Considere um capacitor de placas paralelas cuja a área das placas é e cuja distância entre as placas é . Um dielétrico de constante dielétrica e espessura , com e , encontra-se centralizado entre as placas do capacitor. Suponha que a carga do capacitor seja , com a placa superior positiva e a placa inferior negativa, como ilustrado na figura abaixo. Despreze efeitos de borda.

(a) Sem precisar demonstrar, escreva a capacitância para os casos e .

(b) Sem precisar demonstrar, e para um valor de qualquer, indique: (i) o sinal das cargas induzidas nas superfícies superior e inferior do dielétrico; (ii) e a direção do campo elétrico em todas as regiões entre as placas do capacitor.

(c) Determine o módulo do campo elétrico dentro do dielétrico e entre o dielétrico e as placas do capacitor, para um valor de qualquer.

(d) Determine a capacitância do capacitor para um valor de qualquer.

(e) Encontre a carga induzida na superfície superior do dielétrico.

Das afirmativas abaixo, assinale a única que é incorreta.

1. O campo elétrico produzido por um corpo com carga total igual a zero pode ser diferente de zero;
2. O campo elétrico no interior de um material dielétrico é sempre zero, mesmo que ele esteja em uma região com campo elétrico;
3. O campo elétrico entre as placas de um capacitor isolado diminui quando a região entre suas placas é completamente preenchida por um material de constante dielétrica ;
4. Quando um material dielétrico é inserido entre as placas de um capacitor, surge uma densidade superficial de carga induzida nas superfícies do dielétrico que causa a mudança da capacitância;
5. Quando um material dielétrico é inserido entre as placas de um capacitor, é possível submeter esse capacitor à maiores diferenças de potencial, sem que ocorra a ruptura dielétrica.

Na figura abaixo, dois capacitores de placas planas e paralelas e são ligadas em paralelo a uma bateria de . A área das placas dos capacitores é de e a distância entre as placas é de .

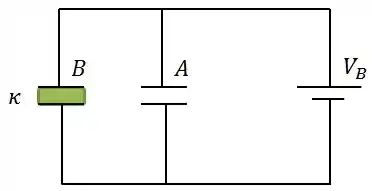
O dielétrico do capacitor é o ar, o do capacitor é um material de constante dielétrica igual a  .

Determine o módulo do campo elétrico:

1. No espaço entre as placas do capacitor ;
2. No espaço entre as placas do capacitor ;

Determine a densidade de cargas livres

3. Na placa de maior potencial do capacitor ;
4. Na placa de maior potencial do capacitor ;
5. Determine a densidade de cargas induzida na superfície superior do dielétrico do capacitor .

Quando se coloca um dielétrico no interior de um capacitor carregado com carga , a capacitância dele se altera e teremos:

1. Campo elétrico nulo no interior do capacitor;
2. Campo elétrico no interior do capacitor aumentará devido ao dielétrico ser polarizável;
3. A capacitância diminuirá;
4. Campo elétrico no interior do capacitor diminuirá devido ao dielétrico ser polarizável;
5. A capacitância do capacitor se tornará nula.

Um capacitor de placas paralelas é carregado com uma carga por uma bateria de ddp . Mantendo-se a bateria ligada, uma lâmina de material plástico de constante dielétrica é inserida entre as placas do capacitor, sem alterar as demais propriedades do sistema. A nova carga nas placas e o novo campo elétrico entre elas são, respectivamente:

1. e ;
2. e ;
3. e ;
4. e ;
5. e ;

Um condutor oco, descarregado, contém uma carga puntiforme em sua cavidade, conforme a figura abaixo.

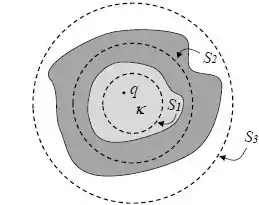
A cavidade é preenchida com um dielétrico de constante dielétrica e a região externa é o vácuo. A figura mostra 3 superfícies gaussianas . Os fluxos, , e , do campo elétrico através das superfícies , e , respectivamente, são dados por:

;;

; ;

; ;

; ;

; ;

Um capacitor de capacitância no vácuo é conectado a uma bateria que sustenta uma tensão adquirindo, portanto, uma carga . A seguir, o capacitor é desconectado da bateria e um dielétrico de constante é inserido entre suas placas. Os novos valores da capacitância , da carga e da tensão entre as placas serão:

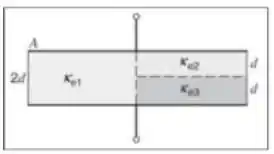
Considere um capacitor de placas paralelas preenchido por três dielétricos distintos , conforme demonstrado na figura abaixo. Sabendo que a distância entre as placas é e a área delas é , calcule a capacitância desse capacitor. Considere

Um capacitor, formado por duas placas separadas por uma distância , possui capacitância . Este capacitor está ligado a uma bateria de . Uma lâmina de Teflon é introduzida entre as placas, sem desconectar a bateria.

O Teflon tem constante dielétrica e rigidez dielétrica igual a . Podemos afirmar que:

A diferença de potencial entre as placas vale e o capacitor deixará de funcionar.

A diferença de potencial entre as placas vale e a nova capacitância será .

A diferença de potencial entre as placas vale e a nova capacitância será .

A diferença de potencial entre as placas vale e a nova capacitância será .

A diferença de potencial entre as placas vale e a nova capacitância será .

Um capacitor carregado tem um campo elétrico de módulo e uma diferença de potencial entre suas placas. Sem conectar nenhuma fonte de , inserimos um material dielétrico entre as placas produzindo um campo elétrico de módulo e uma diferença de potencial através do capacitor. Que afirmativa melhor representa as relações entre os campos elétricos e as diferenças de potencial?

;

;

;

;

;

;

(A) A carga aumenta e a energia do capacitor diminui,

(B) A carga permanece a mesma e a energia do capacitor diminui,

(C) A diferença de potencial diminui e a energia do capacitor aumenta

(D) A diferença de potencial aumenta e a energia do capacitor aumenta

(E) A diferença de potencial permanece a mesma e a energia do capacitor aumenta

Um capacitor plano de placas paralelas é carregado a um potencial . Um dielétrico de constante dielétrica é inserido de modo a preencher o espaço entre as placas do capacitor, e a diferença de potencial entre as placas permanece constante.

Qual das seguintes afirmações a respeito dessa situação é falsa?

a densidade de energia permanece inalterada;

a capacitância é multiplicada por 4;

a energia armazenada é multiplicada por 4;

a carga do capacitor é multiplicada por 4;

o campo elétrico entre as placas é multiplicado por 4;