Energia Cinética + Energia Gravitacional + Energia Elástica

Teoria

Bom, a gente sabe que energia mecânica é:

Lembre-se que

O que vamos fazer agora é trabalhar com as duas energias potenciais ao mesmo tempo. A ideia é a mesma dos outros problemas, só que agora vamos envolver mais de uma incógnita. Quer ver?

(FATEC 2002) Um bloco de massa 0,60kg é abandonado, a partir do repouso, no ponto A de uma pista no plano vertical. O ponto A está a 2,0m de altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m. São desprezíveis os efeitos do atrito e adota-se g=10m/s2. A máxima compressão da mola vale, em metros, é:

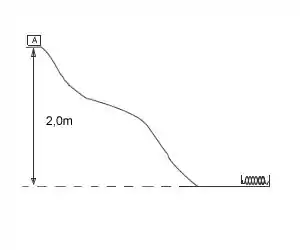
Viu que o bloquinho não sofre nenhuma força não conservativa durante o trajeto né? Então podemos dizer que tanto a energia mecânica no ponto do alto do morro e a energia quando a mola está comprimida são iguais.

Sabendo que:

Vamos calcular + . Como em nenhum dos dois momentos o bloquinho está se movendo, ele não vai possuir energia cinética em nenhum dos pontos.

Igualando as duas expressões:

E assimmmm,

tanammmmmm

Agora é contigo, qualquer coisa me grita! ;)

Exercícios Resolvidos

Exercício Resolvido #1

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 216

Um bloco de é empurrado contra uma mola de massa desprezível e constante , comprimindo a mola até uma distancia igual a . Quando o bloco é libertado, ele se move ao longo de uma superfície horizontal sem atrito e sobre um plano inclinado de . a) Qual a velocidade do bloco enquanto ele desliza ao longo da superfície horizontal depois de abandonar a mola? b) Qual a distancia máxima que ele atinge ao subir o plano inclinado até parar antes de voltar para a base do plano?

Passo 1

Como não temos atrito atuando vamos ter a conservação da energia mecânica. Precisamos calcular a energia mecânica inicial, quando a mola está comprimida. A única energia é a potencial elástica porque ele está parado e vamos considerar a altura inicial como zero.

Passo 2

Vamos agora calcular a energia final, quando ele ainda está na horizontal, que é quando ele solta da mola. Isso nos diz que a única energia é a cinética

Passo 3

As energias são iguais então

Passo 4

Agora o que vai mudar é nossa energia final, porque vamos considerar o final quanto ele atinge a altura máxima para e volta. Isso diz que a energia final é apenas a potencial gravitacional

Passo 5

Vamos igualar a energia inicial que achamos no passo 1

Mas essa não é a distancia percorrida, essa é a altura que ele chegou. Olha a figura abaixo para entender bem a diferença.

Vamos ter

Resposta

Exercício Resolvido #2

TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 232 – 39.

O objeto de é largado do repouso de uma altura de em uma rampa curva sem atrito. Na base da rampa está uma mola com constante de força de . O objeto desliza rampa abaixo e até a mola, comprimindo-a de uma distância até atingir momentaneamente o repouso.

Encontre .
Descreva o movimento do objeto (se ocorrer) após o repouso momentâneo.

Passo 1

Opa! Viu a pegadinha da questão? Claro que não viu! Não tem, hahhahaa

O que vai acontecer na questão é que o bloco vai deslizar pela rampa, ganhar uma velocidade e quando chegar na mola ela vai ser comprimida até parar o bloco. Importante perceber que dois momentos são importantes pra gente: antes do lançamento, quando o bloco ainda está no alto e no momento em que a mola está comprimida.

Como durante o trajeto o bloco ele não perde energia nenhuma, pois não tem forças dissipativas atuando no bloco, podemos conservar a energia nesses dois momentos que são importantes pra gente.

Passo 2

Alternativa a)

Como nos dois momentos importantes pra gente nós sabemos que temos a mesma energia, podemos comparar a energia mecânica dos dois pontos. Vamos chamar de o momento antes do lançamento e o momento depois que a mola é comprimida.

Calculando a energia mecânica dos pontos.

Como o bloco está em repouso, ele não possui energia cinética e também não possui energia elástica, porque não tem nenhuma mola voando ali.

Aqui apesar do bloco quando descer ganhar velocidade, nesse momento ele está parado, ou seja, a velocidade é zero. A mola não ta correndo ali, né? Hahahha

Sendo assim, nesse momento ele não possui energia gravitacional e também não possui energia cinética, só fica com a elástica mesmo.

Passo 3

Como já sabemos a energia mecânica nos dois pontos e que elas são iguais, vamos igualar as equações e descobrir quanto vale o nosso !

Passo 4

Alternativa b)

O que vai acontecer depois? Da mesma forma que a mola parou o bloco, quando ela foi comprimida ao máximo ela vai acelerar o bloco no sentido contrário. Ele vai ficar tão rápido quanto estava antes de chegar na mola e vai subir até a altura que ele partiu no inicio, os iniciais.

Resposta

b) Da mesma forma que a mola parou o bloco, quando ela foi comprimida ao máximo ela vai acelerar o bloco no sentido contrário. Ele vai ficar tão rápido quanto estava antes de chegar na mola e vai subir até a altura que ele partiu no inicio, os iniciais.

Exercício Resolvido #3

UNICAMP- Prova 1-2014.2B- Discursivas 1

Dois blocos estão ligados por um fio leve que passa por uma roldana de massa desprezível e sem atrito. O bloco de massa está sobre uma superfície lisa sem atrito, preso a uma mola de constante elástica , que por sua vez se prende ao bloco de massa . O sistema é solto, a partir do repouso, com a mola sem qualquer deformação.

a) Faça na figura acima um diagrama das forças atuando nos blocos em algum momento após o sistema ser solto.

b) Através do teorema de trabalho-energia, calcule quanto o sistema se desloca até ficar momentaneamente em repouso novamente.

c) Calcule a velocidade do bloco 2 quando este se deslocou a partir do ponto inicial, quando os blocos estão em repouso.

Passo 1

Como não temos atrito, as únicas forças são a tração, a normal, a força elástica e a força peso.

Passo 2

Por conservação de energia mecânica temos que a variação da energia potencial elástica é igual à variação da energia potencial gravitacional. Como eles estão ligados por uma corda, a distensão da corda e a altura são iguais.

Passo 3

Aplicamos novamente a conservação de energia mecânica, mas agora com energia cinética envolvida já que os blocos não atingiram o repouso ainda.

Resposta

Exercício Resolvido #4

UFRJ-Física 1-Prova 1-2012.2-Múltipla Escolha-5

Um pequeno bloco de massa está sobre uma superfície horizontal sem atrito ligado a uma mola de constande elástica cuja outra extremidade é fixa em uma parede, como mostra a figura. O bloco é deslocado para , a partir da posição de equilíbrio, e liberado a partir do repouso. Para qualquer instante posterior, o módulo da sua velocicade é dado por:

Passo 1

Os dados do enunciado são

Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.

Como não temos atrito, não temos trabalho sendo feito então

Passo 2

Temos

Onde

Que foi o quanto a mola ficou deformada.

Então

Passo 3

Onde

Com

Que foi o quanto a mola ficou deformada em um ponto qualquer. Além disso,

Passo 4

Teremos então

Resposta

Letra A

Exercício Resolvido #5

ITA - 2006

Um anel de peso está preso a uma mola e desliza sem atrito num fio circular situado num plano vertical, conforme a figura.

Considerando que a mola não se deforma quando o anel se encontra na posição e que a velocidade do anel seja a mesma nas posições e , a constante elástica da mola deve ser de:

Passo 1

DEUS DU CÉU, VISHI MAINHA, OH MY JESUS, QUE QUI TA ACONTECENU AQUI.

Calma filho, ta tudo calmo, ta tudo 2. O que ta acontecendo aqui é que nós temos um anel que fica rodando nesse círculo ai e tem uma mola presa ali. Alí ó , naquele pontinho ali! Ela não sai dali, sacou?

E olha que maneiro, o que ta variando direto ali é a velocidade, mas em dois pontos o problema falou que a velocidade é igual! Vamos usar esses dois pontos pra ficar mais fácil, pode ser?

Além disso, vamos usar esses dois pontos porque novamente não tem forças dissipativas atuando no anel. Se não tem, é só conservar energia nos dois pontos que ta tudo tranquilo.

Vamos usar o ponto como referência, fechou?

Passo 2

Calculando a energia no ponto :

Lembrando que como a mola não está deformada no ponto , a mola tem comprimento de cm. O que importa aqui é a variação!!

Passo 3

Calculando a energia no ponto P:

Passo 4

Fica atento ali nas unidade , ein? Sempre temos que trabalhar em metros!!!

Como sabemos que os dois tem a mesma energia, vamos igualar as duas equações que achamos e encontramos o valor de !

Resposta

Exercício Resolvido #6

TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 234 – 59.

Um pêndulo está suspenso do teto e preso a uma mola que, por sua vez, está presa ao chão em um ponto diretamente abaixo do suporte do pêndulo. A massa da bolinha do pêndulo é , o comprimento do pêndulo é e a constante da força é . O comprimento da mola frouxa é e a distância entre o chão e o teto é . O pêndulo é puxado lateralmente, de modo a formar um ângulo com a vertical e é então liberado do repouso. Obtenha uma expressão para a rapidez da bolinha, quando ela passa pelo ponto diretamente abaixo do suporte do pêndulo.

Passo 1

Essa questão é no mesmo estilo das que a gente resolveu antes: vamos conservar a energia em dois pontos (um vai ser no momento que ela é solta e o outro é quando ela está diretamente abaixo do suporte) e comparar cada fórmula da energia mecânica, masssss, pera pera pera pera.

Calcular a gravitacional ... a gente sabe, vai ser algo com o ali ..

Calcular a velocidade ... a gente sabe, é a incógnita do problema ...

Calcular a elástica ... opa, pera ai, como faço isso ?

Vamos puxar um pitagoras, mas calma que a gente vai vendo durante a questão!

Passo 2

Vamos escolher o ponto mais baixo da trajetória como sendo . O que vai acontecer na questão é que a energia gravitacional e a energia elástica que a bolinha possui no ponto vai ser transformada em energia cinética quando chegar no ponto .

Vamos conservar energia nos dois pontos (olha, mais uma vez!) porque não temos forças dissipativas atuando na bolinha.

Passo 3

Pra descobrir a deformação da mola temos que aplicar Pitágoras no triângulo de baixo, só que não temos o cateto horizontal. E como acha? É só aplicar Pitágoras no triângulo de cima! Vamos chamar esse cateto de

Assim

Eu sei que você quer tirar a raiz quadrada desse valor aí mas não precisa por que quando formos usar o teorema de Pitágoras no triângulo de baixo vai aparecer também!