Teoria
O que é Trabalho?
Se imagine na casa da sua avó, ajudando a doce velhinha a arrastar aquela estante velha e pesada para poder limpar atrás aquela poeira do ano passado.

Quando você empurra a estante, quanto mais longe você levar a estante mais você vai ficar cansado. Isso quer dizer que quando você empurra a estante ou você faz forças diferentes?
Não, estamos aplicando a mesma força, mantendo a aceleração constante, o que muda aqui é o trabalho, a energia gasta para empurrar a maldita estante.
A idéia de trabalho, é a quantidade de energia que uma força gasta para deslocar um objeto uma certa distância.

OBS:
A unidade de energia que vamos usar em física é . Ela significa , como trabalho é gasto de energia, trabalho e energia possuem a mesma unidade.
Cálculo do Trabalho de Forças
Normalmente a fórmula de trabalho é
Mas devemos dar uma mudada nela.
Imagina que você está se sentindo meio gordinho e deseja emagrecer. Você que é uma pessoa, como o Expert que vos escreve, preguiçoso então é sempre bom um incentivo.
Dessa forma todos nós cometemos o erro de chamar aquele amigo que malha há 19 anos para nos ajudar.
Ele teve a “brilhante” ideia de que você corra com uma pedra de presa na sua cintura por um fio.

Vamos olhar o trabalho feito na pedra,
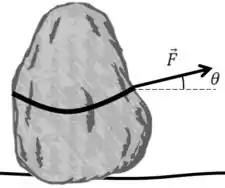
Repara que a força que está puxando a pedra na verdade é inclinada, então só a sua componente horizontal que está realmente puxando a pedra.
A fórmula de trabalho fica, daqui para frente, como.
Onde é a componente da força que realiza trabalho.
Existem alguns casos que devemos olhar.
- Força está na direção e no sentido do deslocamento
- Força está na direção e sentido contrário ao deslocamento
- Força é perpendicular ao movimento
Atenção nesse caso, isso facilita MUITO nossas contas.
Outra forma de calcular o trabalho de uma força é através do produto escalar entre os vetores da força e do deslocamento.
Lembrando do bizu de que o produto escalar pode ser reescrito como
Por isso que quando temos vetores perpendiculares, o trabalho realizado é o zero. Se lembra de alguma força assim? Já ouviu falar que a força centrípeta não realiza trabalho? Já ouviu falar que a força normal quando um bloco desce um plano inclinado também não realiza trabalho?
Justamente pelos vetores força e deslocamento serem perpendiculares essas forças não realizam trabalho.
Além do caso em que as forças são perpendiculares, o trabalho também é zero quando não existe deslocamento.
Deu pra pegar todas as informações daqui? Então #PartiuExercitar!
Cálculo do Trabalho de Forças
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 191 – 24.
Uma caixa de é levantada de uma altura de , a partir do repouso, por uma força aplicada vertical de . Encontre o trabalho realizado sobre a caixa pela força aplicada.
Passo 1
Leu a questão, né? Como a gente tá intímo, vou te chamar no Messenger pra gente bater um papinho, jaé?
Tu já sabe tudo maluco!
ahahhahaha
Passo 2
Agora que você já sabe, vamos pras contas!
Resposta
Exercício Resolvido #2
Trabalho e Energia Cinética
Um disco horizontal gira em torno de um eixo vertical que passa pelo seu centro, com velocidade angular constante. Coloca-se um corpo de pequenas dimensões e massa sobre o disco a uma distância de do seu centro. Verifica-se que o atrito entre o corpo e a superfície do disco é suficiente para que ele permaneça na mesma posição do disco em que foi colocado. Ou seja, ele não desliza sobre o disco. O disco dá uma volta completa no intervalo de tempo . Sabendo-se que o coeficiente de atrito estático entre o corpo e a mesa é , o trabalho realizado pela força de atrito numa volta completa é igual a:
Passo 1
A força de atrito é a força que faz o papel de força centrípeta.
Então ela é perpendicular ao movimento, e seu trabalho é zero.
Resposta
Letra A
Exercício Resolvido #3
Trabalho e Energia Cinética
A figura mostra uma bola de massa rolando sem deslizamento numa trajetória espiral descendente no interior de um cone oco e numa região de campo gravitacional uniforme . O trabalho realizado pela força de contato da parede sobre a bola é:
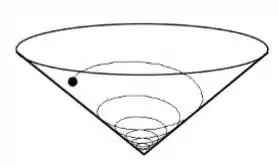
(a) zero.
(b) depende da aceleração gravitacional local e da massa da bola.
(c) depende da forma da trajetória espiral
(d) positivo.
(e) negativo.
Passo 1
A força de contato da parede sobre a bola, nada mais é que a força normal. Lembrando que o trabalho realizado é calculado a partir do produto escalar da força com a trajetória, em outras palavras, pela fórmula:
Onde é o ângulo entre a trajetória e a força. Quando esses dois fizerem 90° entre si, o trabalho realizado será nulo.
Passo 2
Em todos os casos a força normal é perpendicular a trajetória, vou te mostrar com algo mais básico, se liga nesse plano horizontal.
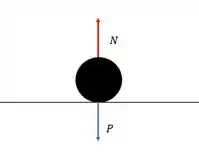
A força normal é perpendicular à trajetória portanto seu trabalho é:
No nosso caso vai acontecer o mesmo, independente desse plano estar inclinado ou não, se liga na figura:
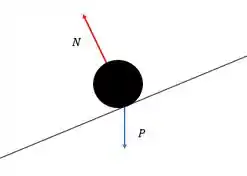
A força normal será sempre perpendicular a superfície, não importa como ela seja.
Então podemos afirmar com 100% de certeza que o trabalho realizado pela força normal na nossa espiral é:
Portanto, o trabalho da força de contato é nulo.
Resposta
Letra (a)
Exercício Resolvido #4
TIPLER, Física, Vol 1,6ª Edição, LTC,2009., pp 193 – ex41
Uma partícula de sofre um deslocamento de Durante esse deslocamento , uma força constante atua sobre a partícula.
- Determine o trabalho realizado por para esse deslocamento.
- Determine a componente de na direção desse deslocamento.
Passo 1
Bom, temos que a definição de trabalho é:
Hmm, temos um produto escalar, mas por quê não usamos aquela velha equação?
Tá querendo me enganar?

Calma, calma! Pode ficar tranquilo que aqui no responde aí, a gente quer trazer sempre a melhor solução!
E nesse caso, vamos resolver o produto escalar multiplicando as componentes de cada sentido dos dois vetores e somando tudo no final.
E vamos usar isso por quê o enunciado nos deu os vetores e suas componentes:
Passo 2
Letra a)
Vamos então fazer o produto escalar aqui, para isso vamos multiplicar as componentes de cada sentido dos dois vetores e somar tudo no final.
Realizando o produto escalar temos:
E o produto dos unitários por eles mesmos vai ser sempre no produto escalar, sendo assim:
Passo 3
Letra b)
Pra calcular a componente, vamos usar a seguinte definição:
Onde é a componente que atua na direção do deslocamento.
Só que a nossa distância aqui é o vetor ,então rearrumando temos:
E agora vamos isolar a parcela que a gente quer, assim teremos:
Agora a gente isolou a componente na direção do deslocamento. Vamos botar os números?
Resposta
Letra a)
Letra b)
Exercício Resolvido #5
Trabalho e Energia Cinética
Uma partícula move-se no plano em uma trajetória retilínea ao longo do eixo , da origem ao ponto , e a seguir ao longo de uma trajetória retilinea do ponto ao ponto , como indicado na figura. Durante todo o percurso agem sobre a partícula três forças constantes , e de mesmo módulo. Os ângulos que as forças , e fazem com o eixo são, respectivamente, , e . Denotando os respectivos trabalhos das três forças em todo o percurso de a por , e , podemos afirmar que
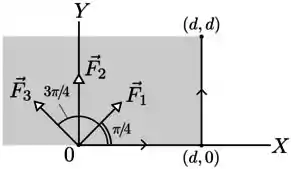
- , e ;
- , e ;
- , e ;
- , e ;
- O trabalho realizado por cada uma das três forças é o mesmo.
Passo 1
Podemos perceber que é na direção do deslocamento, já que ele sobe e vai para a direita, o ângulo que esse deslocamento final faz é que é .
Além disso, a força é perpendicular ao movimento, porque
Podemos perceber também que o ângulo da força com o deslocamento é
Passo 2
Podemos achar então o trabalho de cada força, como nas alternativas ele não se interessa pelo valor, mas sim em comparar os trabalhos de cada força, vamos chamar de a distancia que eles percorrem, não precisamos perder tempo calculando essa distancia.
Além disso, vamos chamar o módulo de todas as forças de , já que são iguais
Então
Temos que
Resposta
Letra C