Trabalho de uma Força Variável
Teoria
Por Integral
Fala meu povo, vamos trocar uma ideia sobre um conceito que a gente já conhece só que agora envolvendo integrais, mas porque diabos envolver integrais? Já que o trabalho era dado por:
Em alguns casos como no exemplo que a gente vai ver não é possível calcular da maneira antiga e isso rola porque a força varia ao longo do caminho, se liga aqui:
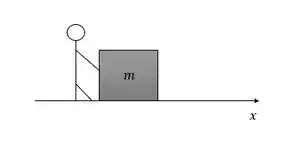
Imagina que o Sr. José empurra uma caixa ao longo do caminho com uma força que varia ao longo do percurso no eixo segundo a função . Qual é o trabalho realizado se a distância percorrida é 100m?
Pra esses tipos de caso, a gente usa a seguinte equação:
Repare que aqui temos a integral de um produto escalar lembrando que esse produto pode ser reescrito como:
Onde é o ângulo entre as forças, e no caso do Sr. José a força que ele aplica é paralela a distância sendo assim , e , então a nossa integral fica para essas situações:
E agora podemos substituir os limites de integração e a função da força:
E resolvendo a integral teremos:
E enfim:
Outro caso interessante é o caso da mola, a própria força da mola já é em função da distância, saca só:
Pra calcular o trabalho realizado por essa mola vamos substituir a força dentro da integral
E aqui a força é paralela a distância portanto a gente pode fazer como para o primeiro exemplo e dizer que:
E enfim substituindo o valor de :
Passando os limites de integração temos:
Como geralmente a mola parte do , fica com aquela formulazinha conhecida:
Qualquer tipo de trabalho de força elástica pode ser encontrado dessa forma.
Um caso mais complicado é quando a força atua em duas direções, imagina alguém puxando uma caixa numa rampa diagonal com a força sendo dada por num plano liso como mostra a figura:
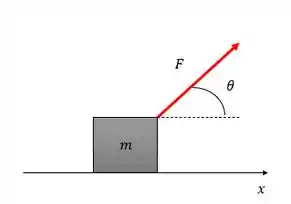
Aqui o nosso problema é bem interessante, a nossa força varia em mas a força em é constante vamos dividir esse cálculo em duas parcelas decompondo as forças dessa forma: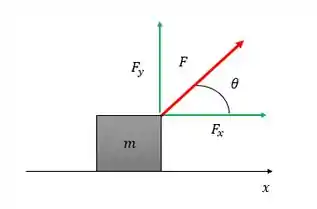
Aqui o trabalho realizado em:
Onde a força é paralela a distância e como vimos no começo da teoria podemos dispensar a notação de produto escalar.
Um bizu supeeer importante é que a força em não gera trabalho na distância em e vice-versa justamente por causa daquele produto escalar que foi falado:
Se a força está na direção e a distância na direção teremos um ângulo de entre os vetores e .
Então aqui podemos substituir nossos valores e aí:
E enfim:
Por área
Tem outra forma muito maneira que a gente pode usar também! Tu que é um bom cara de cálculo, o que te lembra integral, hein? Lembra área!
Nãooooo !!! Essa aí é a área do goleiro, hahahaha.
A forma de calcular o trabalho é calcular a área embaixo do gráfico , vamos encontrar quanta energia ou trabalho gasta uma máquina que aumenta constantemente a força e depois se estabiliza como mostrado no gráfico abaixo.
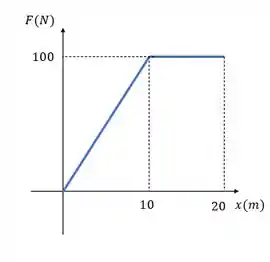
E aqui é muiiito de boa, você pode calcular um trapézio ou a área de um triângulo e a de um retângulo e somar as duas, pelo trapézio a gente tira direto o valor:
E substituindo:
Então temos:
Por área
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 190 – 7.
Como você compara o trabalho realizado para esticar uma mola de , a partir da configuração frouxa, com o trabalho necessário para estica-lá de , a partir da configuração frouxa?
Passo 1
Bom, antes de comparar o trabalho de duas deformações diferentes temos que saber a fórmula do trabalho de uma mola, certinho?
Lembrando que o sempre tem que estar em metro!
Passo 2
Agora vamos calcular o trabalho em cada uma das deformações:
- Deformação de
- Deformação de 1cm
Passo 3
Comparando as duas fórmulas de trabalho, percebemos que o trabalho da deformação de é 4 vezes menor que o trabalho da deformação de .
Resposta
Exercício Resolvido #2
Elaboração Própria
Uma força é aplicada ao longo de , essa força é variável. Podemos ver na figura abaixo a força ao longo dessa distância. Sabendo que o trabalho total é determine o valor de indicado no gráfico.
Passo 1
Para achar o trabalho vamos calcular a área do gráfico.
Podemos separar essa área em 4 partes para facilitar nossas contas
Passo 2
A área 1 é um trapézio, onde a base maior é a base menor é e a altura é .
Vamos ter
Passo 3
A área 2 é um retângulo de lados e . Então:
Passo 4
A área 3 é um triangulo, onde a base é e a altura é .
Vamos ter
Passo 5
A área 4 é um triangulo, onde a base é e a altura é 5.
Vamos ter
Passo 6
A área total via ser
Como essa área é o trabalho total
Resposta
Exercício Resolvido #3
PUCRIO-Física I-Prova 2-2013.1-Questão 1-b
Um bloco ( é arrastado sobre um plano horizontal e seu movimento é estudado durante o deslocamento desde até , com . Uma força é aplicada fazendo um ângulo em relação à horizontal. Considere .
Considere que o módulo de tem valor constante e igual a durante o deslocamento de até , mas suponha que o ângulo varia com a posição de acordo com o gráfico abaixo. Construa o gráfico de como função de , e com base nisto calcule o trabalho realizado pela força ao longo de todo o deslocamento.
Passo 1
Para determinar o gráfico de por, devemos apenas reproduzir o gráfico do só que multiplicado pela força, ou seja multiplicar por . Se liga!
Para determinar o trabalho realizado pela força, basta calcular a área sob a curva:
Resposta
Exercício Resolvido #4
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 192 – 30.
Uma força atua sobre uma partícula que tem massa de . A força está relacionada com a posição da partícula pela fórmula , onde se x está em metros e está em newtons. Encontre o trabalho realizado por esta força enquanto a partícula se move de até .
Passo 1
Bom, aqui diferente da fórmula de trabalho que estamos acostumados a usar, vamos usar a definição de trabalho pra podermos calcular nesse caso. Se lembra da integral ?
Não essa, hahahahhaha, essa aqui ó
Vamos usar essa definição aqui pois varia de acordo com a posição de , mas fica tranquilo que a gente resolve essa integral rapidinho.
Passo 2
Para calcular o trabalho vamos substituir o valor de na integral
Tirando a constante da integral ficamos
Integral de polinômio é tranquilo, né? É só somar 1 no expoente e dividir pelo novo.
Passo 3
Como ele quer do ponto até , vamos usar esses valores na integração.
Como já descobrimos a integral, ficamos com
Se liga que o trabalho é negativo e isso ocorre por que a força tem o sentido contrário ao do deslocamento. ;)
Resposta
Exercício Resolvido #5
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 192 – 31.
Perto de sua cabana de férias há uma caixa d’água solar (preta) usada para aquecer a água de um chuveiro externo. Por alguns dias, no último verão, a bomba estragou e você teve que, pessoalmente, carregar a água do açude até a caixa, acima. Seu balde tem uma massa de e comporta de água, quando cheio. No entando, o balde tem um furo e, enquanto você o elevava verticalmente com uma rapidez constante , a água escapava com uma taxa constante. Ao atingir o topo, apenas de água restavam.
- Escreva uma expressão para a massa do balde mais água, como função da altura acima da superfície do açude.
- Encontre o trabalho que você realiza sobre o balde para cada 5,0kg de água despejada no tanque.
Passo 1
Bom, aqui está você, em sua cabana de férias,
quando você tem que carregar água para a caixa. O que vai acontecer é que mais uma vez a força vai depender do deslocamento, como vamos ver a seguir, e vamos precisar integrar a expressão mais uma vez!
Passo 2
Alternativa a)
Para calcular a massa do balde já sabemos que ela tem que ser uma reta, porque ele disse no enunciado que a água cai a uma taxa constante, certinho? E já da pra sacar que a constante é negativa, porque no final ele vai ter uma quantidade água menor que no inicio
Como ele quer a partir da superfice do açude, sabemos que quando a altura é zero, o balde tem além dos da água
Quando você está 4 metros acima, só tem mais de água
Juntando os valores que encontramos temos a expressão:
Passo 3
Alternativa b)
Agora ele quer saber o trabalho que eu faço pra cada vez que eu vou lá e encho a caixa d’água. E pra encher a caixa d’água eu vou da posição até a posição certo?
Mas qual força eu to fazendo? Eu to dando energia potencial pra água, to subindo ela
Só que como a massa ta variando vamos ter:
Aquele ali é constante, né? Bota ele pra fora!
Sempre que a força depender de vamos ter que integrar para achar o trabalho!