Elasticidade
Teoria
O que é a Elasticidade?
Fala aí! Vamo começar esse liiindo tópico imaginando uma certa situação:
Imagina que eu tenho uma barra de ferro super resistente na vertical, e que eu sou loucasso e vou estacionar um carro em cima dela, assim ó:
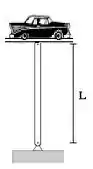
Nós temos uma força muito grande (o peso do carro) sendo aplicada nessa barra... O que será que está acontecendo com nossa barrinha? Ela está aguentando o peso do carro, e pode até parecer que não está acontecendo nada, mas ela está sofrendo uma leve compressão.
Tipo assim:
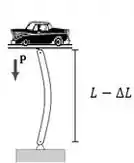
Na prática, nesse caso essa compressão é muuuuito pequena e por isso não conseguimos enxergar a variação do comprimento, o nosso . Por que será que isso acontece? Isso tem a ver com a elasticidade dessa barra, e é isso que vim te explicar nesse tópico!
Na real, o que acontece é que os átomos de um sólido se ligam uns entre os outros, e essas ligações podem ser representadas por molinhas, assim ó:
E essa rede de ligações é quase perfeitamente rígida no caso da nossa barrinha, por isso não percebemos essa compressão que o carro faz na barra, sacou?
Beleza, mas o que significa essa parada de elasticidade?
Bom, o que sabemos é todos os corpos rígidos são ligeiramente elásticos, mas essa elasticidade varia de acordo com o material, o que significa que podemos mudar suas dimensões empurrando ou puxando esse objeto. Então podemos modificar as dimensões de um corpo aplicando uma tensão (que é essa força que puxa ou que empurra) nele. As tensões podem apresentar várias formas diferentes, sendo elas:
- Tração e Compressão
- Cisalhamento
- Tensão Hidrostática
Maaaaas a tensão em todo caso sempre é proporcional à deformação e à uma constante de proporcionalidade, que chamamos de módulo de elasticidade. Show! Então sabemos que:
A deformação pode ser chamada da letrinha , então temos:
Tração e Compressão
Chega cá, tá vendo ali que temos duas forças sendo aplicadas numa área transversal, esticando nosso cilindro? Elas estão fazendo uma tensão no nosso objeto, se liga:
E essa área transversal é sempre a parte de “cima” do que tu quer ver, que no caso do nosso cilindro vai ser uma circunferência. Nossa tensão vai ser calculada pela divisão da Força pela Área e o módulo de elasticidade de uma tração ou compressão é chamado de módulo de Young, dado pela letra . Nome bonito né? A tração acontece quando esticamos o mateiral, e a compressão quando apertamos ele, assim:
A nossa deformação é dada pela deformação dividida pelo comprimento inicial, tipo uma porcentagem, sacou? Como já vimos antes, também podemos chamar essa deformação de . Então:
E, substituindo na equação da proporcionalidade ali em cima, temos:
Então vamos pra um exemplo pra ver se tu entendeu mesmo, sabichão.
Digamos que temos um tubo fechado de um material cujo módulo de elasticidade seja 2MPa (Mega Pascais). Agora vamos causar uma força de compressão nesse tubo, que tem formato cilíndrico com área transversal de . Sabendo que a deformação causada por essa força foi de 0,05, como que a gente calcularia o módulo dessa força aplicada?
E aí, vamo nessa?
Temos a área, a deformação e o módulo de elasticidade, então:
Substituindo a nossa deformação, o módulo e a área transversal do nosso tubo, temos:
Conseguimos! Lindu dimai mãe!
Cisalhamento
Bom, nesse caso aqui a diferença é que a força não vai mais ser perpendicular a área transversal, e sim no mesmo plano da área, sacou? Como temos uma força cisalhante, nosso módulo de elasticidade agora pode também ser chamado de módulo de cisalhamento (G). Então temos algo assim:
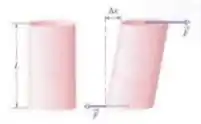
Como vemos pela imagem, nossa deformação não acontece mais no comprimento L, agora temos uma deformação , no mesmo plano da área. Então:
Bem parecido com o anterior, né? Fazer uns exercícios depois que é showww!
Tensão Hidrostática
A tensão nesse caso vai ser a pressão que um fluido vai exercer num objeto submerso, ou seja, a tensão hidrostática, que é algo que acontece quando temos um objeto dentro d’água, por exemplo, sacou?
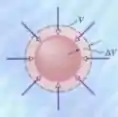
Como a gente tem forças sendo exercidas em todos os lugares do objeto, na realidade teremos uma compressão volumétrica, sacou? Então nossa deformação vai ser o mesmo que vimos na tração e compressão, mas em relação ao volume, assim:
E aqui nesse caso, só pra diferenciar, vamos chamar o módulo de elasticidade da letrinha agora. Então, mesma coisa:
Gráfico Tensão x Deformação
Outro ponto importante de ressaltar é que quando analisamos um gráfico relacionando a tensão com a deformação, temos algo assim:
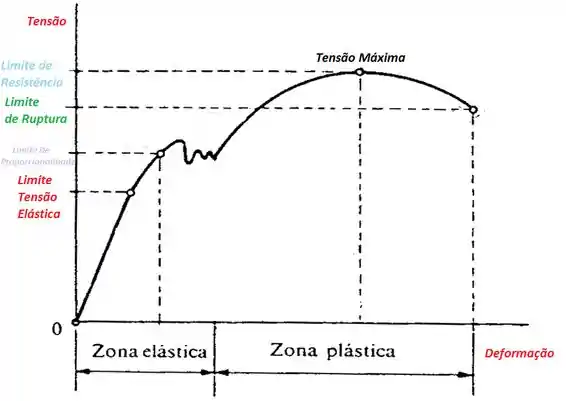
Bom, vamos entender cada nome desses então. A zona elástica é a zona onde depois que paramos de fazer a tensão, as dimensões voltam pra original, tipo uma mola. Quando a gente estica a mola ela se deforma, mas quando soltamos ela, ela tende a voltar pra sua posição inicial. Sacou? Já a zona plástica é quando aplicamos uma tensão e as dimensões não retornam a original. Tudo que estudamos nesse tópico, a parada do módulo de elasticidade, vale até aquele Limite de Proporcionalidade, que é exatamente até onde a Tensão é proporcional a deformação, por isso temos um gráfico linear, ta vendo?
E analisando exatamente essa parte elástica, podemos ver que nosso módulo de elasticidade é exatamente o coeficiente angular do gráfico, sendo assim calculado por:
Massa demaisss!
Então vimos todos os tipos de tensão e assim acabamos o módulo de elasticidade! Agora vamos fazer uns exercícios pra aprender melhor e fixar bem todo o conteúdo!:D
Tração e Compressão
Cisalhamento
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
A figura abaixo mostra a curva típica de um comportamento elástico de um ensaio de tração.
Nessa curva, o ponto:
- P representa o limite de resistência elástica do material.
- P representa o limite de resistência máxima do material.
- M representa o limite de resistência máxima do material.
- F não representa o ponto de ruptura do material.
- Do ponto P ao ponto M aé o intervalo de deformação permanente.
Passo 1
Como a gente viu na teoria, a parte linear do gráfico (apesar de feio) SEMPRE represente a resistência elástica do material. Então P representa o limite elástico do mesmo! Showww!
Resposta
- P representa o limite de resistência elástica do material.
Exercício Resolvido #2
CESGRANRIO 2011 - Petrobras
Em um ensaio de tração, um corpo de prova é submetido a um esforço que tende a alongá-lo até a ruptura. Nesse ensaio de tração, a(o)
- tensão de tração é o quociente entre a carga mecânica aplicada no ensaio e o comprimento inicial do corpo de prova.
- deformação é o quociente entre a alteração de tamanho do corpo de prova e o comprimento inicial.
- estricção ou empescoçamento é o quociente entre a alteração de tamanho do corpo de prova e o comprimento inicial do corpo de prova.
- velocidade do ensaio pode afetar a tensão de escoamento.
- módulo de elasticidade ou módulo de Young corresponde à inclinação da curva tensão-deformação na região plástica.
Passo 1
Lembrando a nossa formulinha que vimos na teoria, a tensão é dada por:
O que já anulamos a letra a e c. Na letra d falamos de velocidade... Mas tu tá vendo velocidade na formulinha? Não né? Então também tá falsa! E na letra e, sabemos que o módulo é a inclinação na curva na região elástica!
Então, é a deformação, lembra? Então já gabaritamos a letra b!
Resposta
(b) deformação é o quociente entre a alteração de tamanho do corpo de prova e o comprimento inicial.
Exercício Resolvido #3
exerciciosengenharia.com
Um pedaço de cobre originalmente com 300 mm de comprimento (Lo = 300 mm) é puxado em tração com uma tensão de 270 MPa (τ =270MPa). Se a sua deformação é inteiramente elástica, qual será o alongamento resultante (em mm)? O modulo de elasticidade E é de 108000 MPa.
Passo 1
Como a gente viu lá na teoria, temos que a tensão é dada por:
Como queremos o resultado em milímetros, podemos deixar os 300 no comprimento inicial, então:
Então houve um alongamento ! Show!
Resposta
Exercício Resolvido #4
NUCEPE 2018
Um pedaço de alumínio é tracionado com uma tensão de 250 MPa e atinge alongamento resultante de 0,77 mm aproximadamente. O módulo de Elasticidade do alumínio EAl = 69 GPa. Se a sua deformação é inteiramente elástica, seu comprimento inicial (l0) era aproximadamente de:
- 233mm
- 212mm
- 305mm
- 276mm
- 110mm
Passo 1
Bora lá!
Então a questão já nos deu tudo e pediu , né? Simbora!
Showwww!
Resposta
b) 212mm
Exercício Resolvido #5
PMT3100 2017
Fios de aço carbono com área de seção transversal nominal de 62,9 mm2 são utilizados para a fabricação de peças pré-moldadas de concreto protendido. Nessas peças, a armação de fios de aço é pré-tensionada (tração) antes de ser imersa na matriz de concreto. Depois que o concreto é adicionado e endurece, a tensão na armação de aço é relaxada; o aço sofre recuperação elástica e comprime o sistema todo, o que aumenta a resistência mecânica do conjunto, pois mantém o concreto sob um esforço de compressão. O valor do módulo de elasticidade desse aço é 200 GPa. Assumindo que esses fios de aço sofreram uma deformação elástica de 1% quando foram pré-tensionados, qual foi a força (em newtons) à qual eles foram submetidos no processo de pré-tensionamento?
Passo 1
Então, temos:
Como a deformação foi 1%, a razão entre a variaçõ e o comprimento inicial será 0,01, né?
Então:
Fechouuuu!
Resposta
Exercício Resolvido #6
PMT3100 2017
Um pedaço de arame recozido de aço baixo carbono tem 2 mm de diâmetro, limite de escoamento (elásticidade) 210MPa e módulo de elasticidade 207GPa. Pergunta-se:
a) Se uma garota de 54 kg se dependura neste arame, ocorrerá deformação plástica (defor no arame?
b) Se for possível com os dados disponíveis no problema, calcule o alongamento porcentual do arame com a garota dependurada.
Passo 1
Como a gente viu lá no graficozinho, a deformação plástica (ou faixa permanente) é logo após o limite de elasticidade, né? Então como a gente tem a massa da garota, é so analisarmos a tensão que a força Peso dela vai exercer no arame de aço e vermos se essa tensão é superior ao limite, show? Vamo lá:
Agora é só calcular a tensão!
Como o módulo da nossa tensão é menor que o limite elástico (210MPa) não ocorre deformação plástica, apenas elástica! Simboraaaa!
Passo 2
Agora calcular a porcentagem da deformação ficou fácil, né? Bora lá:
Chamando o alongamento de , temos:
Como queremos em pocentagem, é só multiplicarmos por 100, então temos:
Resposta
Exercício Resolvido #7
FGV 2018
A figura a seguir ilustra três barras de seção quadrada com lado igual a 10 cm posicionadas entre os cabeçotes de uma prensa hidráulica. Duas barras são constituídas por um material B e a outra por um material A.
Sabe-se que o material A possui módulo de elasticidade igual a 200 GPa, enquanto o material B possui módulo de elasticidade igual a 100 GPa. Além disso, a distância entre os cabeçotes, L, é igual a 1,0 m.Ao se impor uma carga P igual a 2000 kN, calcule a deformação específica provocada por essa força em % apenas em A.
Passo 1
Então, como a gente já sabe:
A questão quer a deformação... Então ela quer esse termo aqui ó:
Então pra descobrir esse termo, precisamos do módulo de elasticidade (que a questão já nos deu) e da tensão, que não temos, mas temos a força e podemos calcular a área tramsversal, sacou? Como a áre transversal é quadrada e de lado 0,1m, temos que a área é 0,01. Show! Então nossa tensão é:
Show, né? Agora como queremos a deformação em A, é só usarmos o módulo de elasticidade do material A:
Então a deformação foi de . Pequenininha, né não? :p
Resposta
Exercício Resolvido #8
UFPA 2018
Um cabo de aço de 2 mm de diâmetro, que tem limite de escoamento de 210 MPa e módulo de elasticidade de 210 GPa, é utilizado para sustentar um bloco cujo peso é de 600 N. Nesta condição, pergunta-se a um engenheiro mecânico se ocorrerá deformação plástica no cabo de aço e qual o alongamento percentual aproximado do cabo de aço com o bloco suspenso. A resposta correta do engenheiro mecânico é: Adotar (π = 3).
- Não ocorrerá deformação plástica e o alongamento percentual é de 0,0952%.
- Não ocorrerá deformação plástica e o alongamento percentual é de 0,0872%.
- Ocorrerá deformação plástica e o alongamento percentual é de 0,0952%.
- Ocorrerá deformação plástica e o alongamento percentual é de 0,0872%.
- Ocorrerá deformação plástica, não sendo possível calcular o alongamento percentual com as informações dadas.
Passo 1
Então...
Pra descobrirmos de houve ou não deformação plástica, é só analisarmos se a tensão superou o limite de escoamento, lembra? Então vamo lá, primeiro vamos calcular a área transversal:
E nossa força é 600N, então:
Então não ultrapassamos o limite de escoamento, que é 210MPa! Isso significa que a deformação é elástica e não plástica. Show!
Passo 2
Agora que já temos a tensão e a questão nos deu o módulo de elasticidade, é só a gente calcular a deformação! Simbora:
Showwwww!
Resposta
- Não ocorrerá deformação plástica e o alongamento percentual é de 0,0952%.