Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Equilíbrio Estático

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender tudo sobre Equilíbrio Estático com o Responde Aí!?

O que é Equilíbrio Estático?

O equilíbrio estático acontece em um corpo parado quando o somatório de forças que agem sobre ele é igual a zero!

Um exemplo clássico de equilíbrio estático é a Torre de Piza, na Itália. Ela tem essa inclinação que parece que vai cair, mas a verdade é que ela esta super firme!

Torre de Pisa: Equilíbrio Estático
Torre de Pisa: Equilíbrio Estático

Nesse vídeozinho abaixo a gente explica tudo o que você precisa saber sobre o Equilíbrio Estático pra você arrasar na sua prova! 👇

📢 Clique para saber mais:

Condições para Equilíbrio Estático

Para um corpo ser considerado em equilíbrio estável são necessárias duas condições:

  • O somatório das forças externas ser zero
  • O somatório dos torques externos em relação a qualquer ponto ser zero

A primeira coisa importante de ressaltar é que um corpo é diferente de uma partícula. Uma partícula tem dimensões desprezíveis, enquanto um corpo tem dimensões bem definidas. Em diversos campos da Física, trabalhamos com partículas. No estudo de estática, trabalharemos com corpos.

Somatório de Forças Igual a Zero

Considere o objeto da figura abaixo, em equilíbrio estático:

Objeto em equilíbrio estático
Objeto em equilíbrio estático

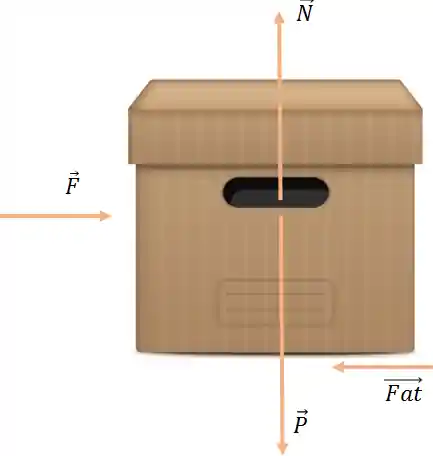
Uma das condições para a caixa da figura acima estar em equilíbrio estático é que a força peso e a força se anulem e que a força e a força de atrito também se anulem. Isso garante que o somatório de forças seja zero.

Assim, concluímos que para que a força resultante seja zero, o somatório de forças deve ser zero tanto no eixo , quanto no eixo .

Somatório de Torques Externos Igual a Zero

Uma das condições necessárias para a existência de um equilíbrio estático é que o torque resultante seja zero!

O torque de um corpo, também chamado de momento, é a grandeza que mede a intensidade que faz um corpo girar. Ele é dado pelo produto vetorial entre o vetor posição e o vetor força.

Na maioria das vezes, podemos simplesmente calcular o módulo do torque e pensarmos no sentido do giro. O módulo é dado pela seguinte fórmula:

Ou seja, o vetor força e o vetor posição fizerem, entre si, um ângulo de . A fórmula se reduz a:

Onde é a distância da aplicação da força até o ponto de rotação. É importante ressaltar que em alguns casos pode ser útil calcular o momento em relação a um eixo.

Podemos exemplificar da seguinte forma. Na figura abaixo há uma barra de massa desprezível em cima de um apoio triangular em equilíbrio estático.

Barra em equilíbrio estático
Barra em equilíbrio estático

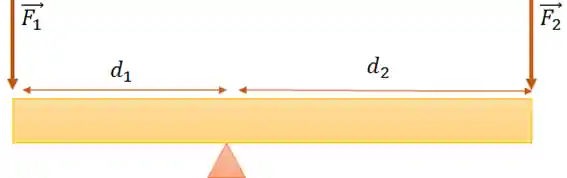
Para que a condição do torque resultante ser igual a zero seja satisfeita, é necessário que o momento provocado por em relação ao ponto de apoio se anule com o momento provocado por em relação a esse mesmo ponto.

Percebemos que o sentido de giro de é horário e o sentido de giro de é anti-horário.

Por convenção, normalmente, definimos o sentido anti-horário como positivo. Sendo assim, se a barra está em equilíbrio estático, podemos montar a seguinte equação:

Pronto! A equação de torque resultante no equilíbrio estático está montada. Dependendo das incógnitas dos problemas, pode ser necessário montar um sistema com o torque resultante e as forças resultantes.

Exemplo: Escreva as condições para o equilíbrio estático da seguinte barra

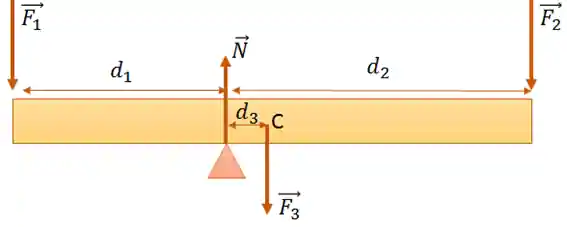
Exemplo: Equilíbrio estático
Exemplo: Equilíbrio estático

Aqui temos a mesma barra da questão acima, apoiada em um suporte triangular em equilíbrio estático. A diferença é que temos a normal e a o peso da barra não é desprezível, ou seja, podemos colocar toda força peso concentrada em um único ponto: o centro de gravidade.

Usaremos, então, as equações de força resultante e torque resultante. Como só temos forças no eixo , calcularemos apenas nesse eixo.

Escolhendo o ponto de apoio como eixo de rotação, podemos montar também a equação de momento.

Quando escolhemos o ponto de apoio como eixo de rotação, o momento da reação é nulo, pois a linha de ação da força passa pelo ponto de rotação. Podemos pensar, também, que a distância vai ser nula.

Agora vamos praticar com exercícios?!

Exemplo: Escreva as condições para o equilíbrio estático da seguinte barra

Exercícios Resolvidos

Exercício Resolvido #1

TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 422 – 1.

Verdadeiro ou falso:

  1. ∑ F → = 0 é suficiente para que ocorra equilíbrio estático.
  2. ∑ F → = 0 é necessário para que ocorra equilíbrio estático.
  3. No equilíbrio estático, o torque resultante em relação a qualquer ponto é zero.
  4. Um corpo em equilíbrio não pode estar se movendo.

Passo 1

Vamos analisar cada uma das afirmativas:

  1. ∑ F → = 0 é suficiente para que ocorra equilíbrio estático. As condições ∑ τ → = 0 e ∑ F → = 0 devem ser satisfeitas para ocorrer o equilíbrio estático. Não basta apenas uma delas. Falso.
  2. ∑ F → = 0 é necessário para que ocorra equilíbrio estático. Essa condição é necessária para ocorrer o equilíbrio estático. Verdadeiro.
  3. No equilíbrio estático, o torque resultante em relação a qualquer ponto é zero. Para que a condição ∑ τ → = 0 seja satisfeita, o torque resultante em relação a qualquer ponto deve ser zero. Verdadeiro.
  4. Um corpo em equilíbrio não pode estar se movendo. Um corpo em equilíbrio pode se mover desde que esteja com velocidade constante e que as condições ∑ τ → = 0 e ∑ F → = 0 sejam satisfeitas. Falso.

Resposta

  1. Falso
  2. Verdadeiro
  3. Verdadeiro
  4. Falso

Exercício Resolvido #2

TIPLER,P.- Física para Cientistas e Engenheiros Vol 1,6ª Edição, LTC,2009., pp 422 – 2.

Verdadeiro ou falso:

  1. O centro de gravidade está sempre no centro geométrico do corpo.
  2. O centro de gravidade deve estar localizado dentro de um corpo.
  3. O centro de gravidade de um bastão é localizado entre as duas extremidades.
  4. O torque produzido pela força de gravidade, em relação ao centro de gravidade, é sempre zero.

Passo 1

Vamos analisar cada uma das afirmativas:

  1. O centro de gravidade está sempre no centro geométrico do corpo

    2. Temos 3 centros. Centro de gravidade, centro de massa e centro geométrico.

    Para que o centro de massa seja igual ao centro geométrico de um corpo, é necessário que o corpo seja homogêneo, isso é, que a massa esteja uniformemente distribuída.

    E para que o centro de gravidade seja igual ao centro de massa, é necessário que gravidade seja constante o que nem sempre é, portanto a resposta é Falso.

    Passo 2

  2. O centro de gravidade deve estar localizado dentro de um corpo. Nem sempre. Um bom exemplo de um objeto que tem seu centro de gravidade localizado fora do corpo é um donut.

    3. Portanto pra essa alternativa temos Falso.

    Passo 3

  3. O centro de gravidade de um bastão é localizado entre as duas extremidades. A estrutura do bastão e a definição de centro de gravidade garantem que o centro de gravidade esteja localizado entre as duas extremidades. Verdadeiro

    4. Passo 4

  4. O torque produzido pela força de gravidade, em relação ao centro de gravidade, é sempre zero. A linha da força de gravidade, dessa forma, estará passando pelo eixo de rotação definido, o centro de gravidade. Vamos analisar um caso qualquer e entender o motivo.

O torque é dado pela formula:

τ = d → × F → = d F s e n θ

E num corpo qualquer o peso é colocado diretamente em cima do centro de gravidade.

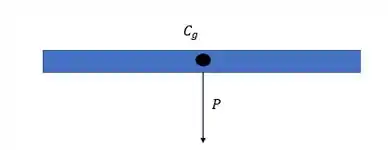
Nesse caso a distância da força até o eixo é 0, fazendo o torque ser 0 também!

τ = 0 × F s e n θ = 0

Portanto para essa afirmação temos Verdadeiro.

Resposta

  1. Falso
  2. Falso
  3. Verdadeiro
  4. Verdadeiro

Exercício Resolvido #3

TIPLER,P.- Física para Cientistas e Engenheiros Vol 1,6ª Edição, LTC,2009., pp 422 - 8

Os velejadores da foto estão usando uma técnica chamada “hiking out”. Qual é o objetivo deles se colocarem na posição mostrada? Se o vento fosse mais forte, o que seria necessário para manter a embarcação estável?

Passo 1

Apesar de estar se movendo, há um equilíbrio estático entre o barco e os velejadores. O objetivo deles se colocarem na posição mostrada é garantir esse equilíbrio. Na figura, é possível perceber que o vento parece estar gerando um torque no sentido horário. Ao se colocarem na posição da figura, os velejadores conseguem aumentar o torque no sentido anti-horário e, assim, garantir o equilíbrio estático do corpo.

Passo 2

Se o vento fosse mais forte, o torque no sentido horário aumentaria ainda mais. Dessa forma, os velejadores deveriam se distanciar o máximo possível do eixo de rotação para aumentar o torque no sentido anti-horário, já que a distância aumentaria.

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma porta homogênea de 18 k g , com 2,0 m de altura e 0,80 m de largura, está presa a duas dobradiças situadas a 20 c m do topo e a 20 c m da base. Se cada dobradiça suporta metade do peso da porta, d
Uma barra fina e homogênea, de massa M , é suspensa horizontalmente por dois fios verticais. Um dos fios prende-se à extremidade esquerda da barra, e o outro fio dista 2 / 3 do comprimento da barra, d
Um alçapão quadrado em um teto tem 0,91m de lado, uma massa de 11k g e está preso por uma dobradiça de um lado e por um ferrolho do lado oposto. Se o centro de gravidade do alçapão está a 10c m do cen
Verdadeiro ou Falso:(a) ∑ i F → i = 0 é suficiente para que ocorra equilíbrio estático.(b) ∑ i F → i = 0 é necessário para que ocorra equilíbrio estático.(c) No equilíbrio estático, o torque resultant
As forças F 1 , F 2 e F 3 agem sobre a estrutura cuja vista superior aparece na figura. Deseja-se colocar a estrutura em equilíbrio aplicando uma quarta força em um ponto como P . A quarta força tem c