Centro de Gravidade
Teoria
Fala aí! Bora bater um papo sobre Centro de Gravidade?!
O que é Centro de Gravidade?
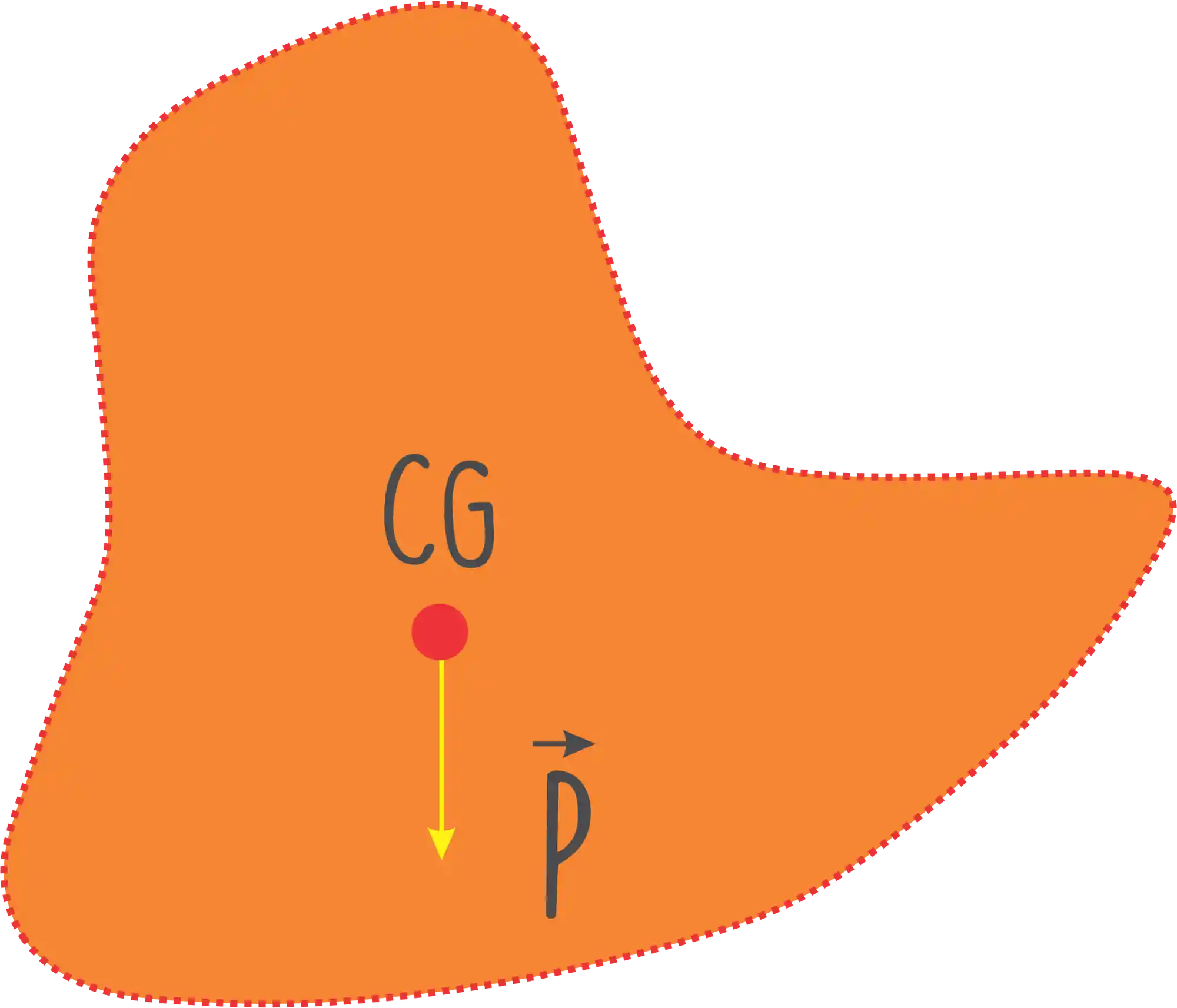
O Centro de Gravidade, também chamado de baricentro é o ponto de um corpo onde podemos considerar que todo o seu peso esteja aplicado.
📢 Clique para ver mais:
- Centro de Gravidade: Exercícios Resolvidos;
- Fórmula do Centro de Gravidade;
- Fórmula do Centro de Massa.
Como Calcular o Centro de Gravidade?
A força gravitacional que age sobre um corpo ou um sistema é a soma vetorial das forças gravitacionais que agem sobre todos os elementos do mesmo. Então pra a gente calcular o centro de gravidade, vamos imaginar um corpo não homogêneo:
Pra a gente achar o centro de gravidade, vamos somar cada componente da força peso e colocar num ponto só, o centro de gravidade, lembrando que a gente tem que definir um eixo de referência pra calcular esse camarada.
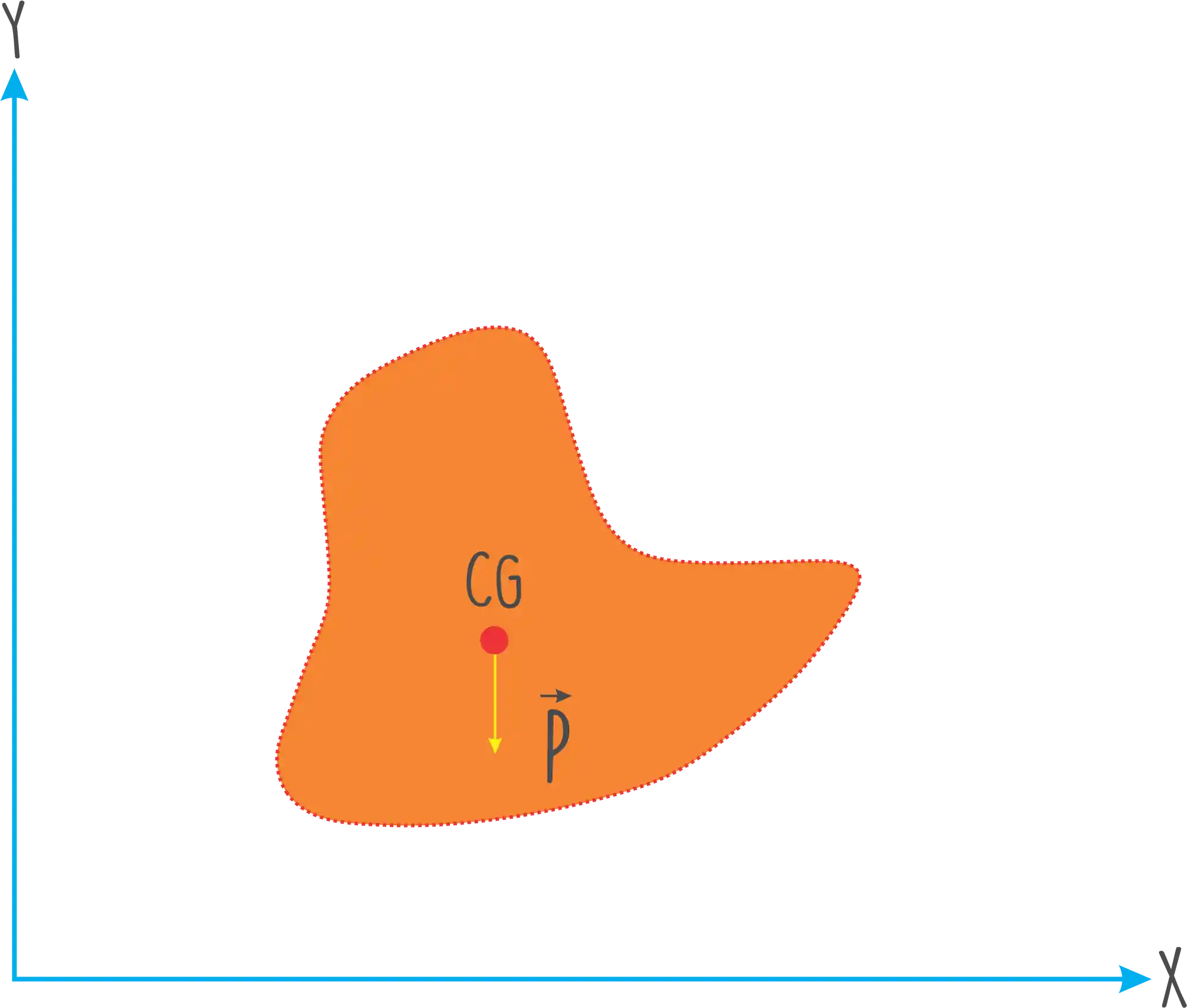
Onde,
-Mas cara, como é que eu faço para calcular o centro de gravidade? 😖
Fórmula do Centro de Gravidade
A fórmula do centro de gravidade tem essa carinha aqui:
O torque resultante do centro de gravidade é igual ao somatório de todos os torques que agem sobre o corpo.
Assim a gente pode isolar a posição do centro de gravidade:
Centro de Massa e Centro de gravidade
O centro de massa tem a mesma ideia do que o centro de gravidade e muitas vezes os dois coincidem. A diferença é que no centro de massa a gente só calcula usando as massas, porém quando a gravidade é constante o cálculo acaba sendo o mesmo!
Vamos calcular o centro de gravidade pra esse sistema com gravidade constante e avaliar isso.
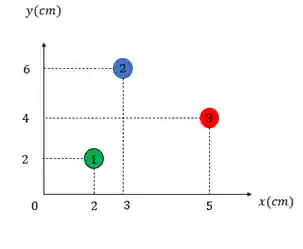
Dados:
Podemos escrever que para cada peso:
Da mesma forma que pro corpo não homogêneo a gente pode usar a seguinte equação pra posição do centro de gravidade:
Podemos cortar a gravidade, já que ela é a mesma para todos os corpos.
Pro nosso caso então só precisamos definir a posição de cada bolinha:
Substituindo:
Calculando:
E representando na figura:
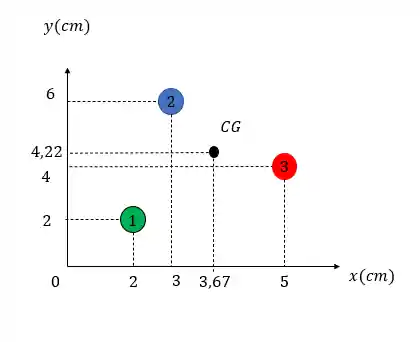
Percebemos então que quando a gravidade for constante, o centro de massa do objeto coincide com o centro de gravidade, já que
Agora vamos praticar com exercícios?!
Centro de Massa e Centro de gravidade
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 422 – 15.
Um automóvel tem 58 por cento do seu peso sobre as rodas dianteiras. O eixo dianteiro e o eixo traseiro estão afastados de 2,0 m. Onde está localizado o centro de gravidade?
Passo 1
Montamos um sistema de coordenadas com a origem passando pelo ponto de contato das rodas dianteiras e de modo que a parte positiva de x inclui o ponto de contato das rodas traseiras. A ideia é algo assim:
Chamando de peso total:
Como está sobre o eixo de rotação, o momento gerado pelas rodas dianteiras é nulo. Assim, chegamos a:
Resposta
84 cm
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 2 , 8º ed. Rio de Janeiro: LTC , 2006, pp 17-1
Como a constante é praticamente a mesma em todos os pontos da grande maioria das estruturas, em geral supomos que o centro de gravidade de uma estrutura coincide com o centro de massa. Neste exemplo fictício, porém, a variação da constante é significativa. A figura abaixo mostra um arranjo de seis partículas, todas de massa , presas na borda de uma estrutura de massa desprezível. A distância entre partículas vizinhas é 2,00 m
A tabela a seguir mostra o valor de (em m/s²) na posição de cada partícula. Usando o sistema de coordenadas mostrado na figura, determine:
- A coordenada do centro de massa do sistema de seis partículas.
- A coordenada do centro de massa do sistema de seis partículas.
- A coordenada do centro de gravidade do sistema de seis partículas.
- A coordenada do centro de gravidade do sistema de seis partículas.
Em seguida, determine:
Passo 1
- Aplicando a fórmula de centro de massa, temos:
Para x temos:
Passo 2
Para y aplicamos a mesma fórmula:
E, assim, chegamos a:
Passo 3
Aplicando a fórmula de centro de gravidade, percebemos que como a gravidade não é constante, ela não vai coincidir com o centro de massa.
Aplicando a fórmula para x:
Passo 4
Aplicando a fórmula para y:
Resposta
a)1,00m
b)2,00m
c)0,987m
d)1,97m