Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 15
As forças , e agem sobre a estrutura cuja vista superior aparece na figura. Deseja-se colocar a estrutura em equilíbrio aplicando uma quarta força em um ponto como . A quarta força tem componentes vetoriais e Sabe-se que , , , , e . Determine (a), (b) e (d) .
Passo 1
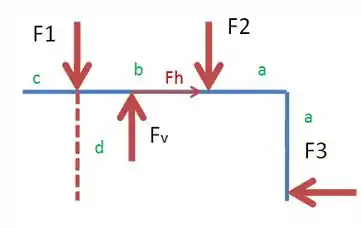
Show de bolinhas pessoal, temos que as forças atuam no sistema de acordo com a figura:
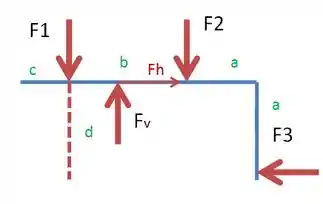
Dessa maneira, vamos primeiro analisar o equilíbrio horizontal do sistema, nesse caso obtemos que:
Passo 2
Já na letra (b), do equilíbrio na vertical, conseguimos obter que:
Logo:
Passo 3
Iradoso, agora na letra (c), basta fazermos o equilíbrio de torques para encontrarmos o valor de . Fazendo o equilíbrio com relação ao ponto O (ponto de aplicação de ), temos:
Isolando :
Portanto, substituindo os valores que o enunciado fornece, obtemos:
Resposta
(a)
(b)
(c)