Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 22
Uma porta homogênea de , com de altura e de largura, está presa a duas dobradiças situadas a do topo e a da base. Se cada dobradiça suporta metade do peso da porta, determine a magnitude e a orientação das componentes horizontais das forças exercidas pelas duas dobradiças sobre a porta.
Passo 1
Então, galerinha do bem, pra fazer essas questões de momento de corpo extenso a gente tem que achar o centro de massa do objeto. Como a porta é homogênea, o centro de massa dela vai ser bem no meio, ou seja, a na horizontal e a de altura.
Outra coisa muito importante é fazer o diagrama de corpo livre. Para isso, precisamos entender as forças atuando no corpo extenso.
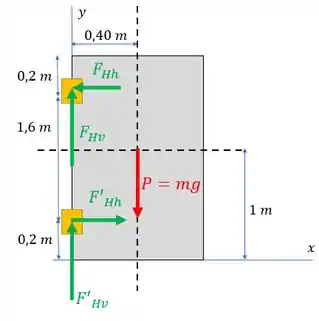
Temos a força peso (em vermelho) atuando no CM da porta. E temos as forças de reação nas dobradiças. Vamos considerar que as dimensões das dobradiças são desprezíveis em relação às da porta. Nelas a gente tem as reações na vertical e as reações na horizontal.
Vamos arbitrar um sentido para as forças horizontais. Se na nossa conta elas ficarem com magnitude negativa é porque o sentido certo é o oposto ao que a gente considerou.
O que o enunciado quer é saber o sentido e magnetude das reações horizontais. A ideia aqui é a gente perceber que a porta está paradinha, então podemos usar as equações de equilíbrio
Vamos lá!
Passo 2
Como a gente não sabe as forças de reação verticais (e nem quer saber), é uma boa a gente usar a equação do torque resultante nas dobradiças da porta. Por que?
Porque e tem a suas linhas de ação passando pelas duas dobradiças. Então elas não geram torque em relação a esses pontos. Assim não precisamos usa-las nas equações do torque nas dobradiças.
Vamos usar então
Em relação à dobradiça de baixo, as únicas forças que geram torque são e , isso porque está aplicada nessa dobradiça, ou seja, nesse ponto, então ela não gera torque.
Considerando o sentido anti-horário como positivo, temos
Isso quer dizer que a força gera torque no sentido anti-horário, e sua linha de ação está distante da dobradiça de baixo. E que gera torque no sentido horário, e sua linha de ação dista da dobradiça de baixo. Substituindo a expressão de :
Isolando e substituindo nossos dados
Percebe que a magnitude de ficou positiva. Isso quer dizer que tem mesmo o sentido que a gente escolheu no diagrama. Ela aponta para a esquerda.
Passo 3
Como a porta está em equilíbrio, a força resultante na horizontal é nula.
Montando essa equação respeitando os sentidos das forças do diagrama, escolhendo a direita como sentido positivo:
Substituindo o que achamos no passo anterior
Mais uma vez o valor deu positivo, então nossa força está no sentido adotado no diagrama. Ela está para a direita.