Lei de Brewster
Produzido por Bruno SoaresTeoria
Polarização da Luz
A luz é uma onda eletromagnética. Ondas eletromagnéticas são um pouco como cordas.
Se você prender uma das pontas, pegar a outra, e ficar chacoalhando, ela vai ficar vibrando pra cima e pra baixo. No caso das ondas eletromagnéticas, quem fica vibrando é o campo elétrico e o campo magnético.
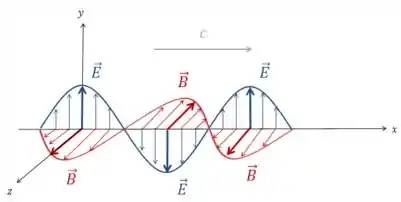
A polarização da luz é a direção na qual o campo elétrico vibra (usamos o campo elétrico e não o magnético por convenção).
Porém, quando a luz é emitida por certas fontes, como o sol, seu campo elétrico vibra em diversas direções aleatórias. Nesse caso dizemos que a luz é não-polarizada.
Polarização por reflexão
A luz não-polarizada pode ser totalmente ou parcialmente polarizada por meio de reflexão.
Antes de prosseguir, vamos chamar o plano formado pelo raio incidente, o raio refletido e a normal à superfície de plano de incidência.
Quando a luz não-polarizada incide sobre a superfície que separa os meios transparentes de índices de refração e , para a maioria dos ângulos de incidência, a luz refletida é parcialmente polarizada.
Porém, existe um determinado ângulo chamado de ângulo de polarização, para o qual:
- A luz refletida é totalmente polarizada em um plano perpendicular ao plano de incidência.
- A luz refratada é parcialmente polarizada em um plano paralelo ao plano de incidência.
Podemos calcular o valor do ângulo de polarização através da Lei de Brewster que nos diz que, quando o ângulo de incidência é igual ao ângulo de polarização , o raio refletido e o raio refratado são perpendiculares
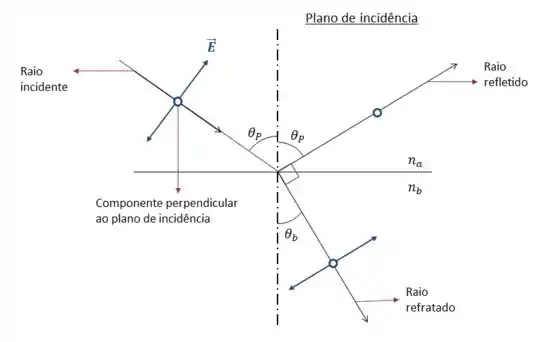
Logo,
De acordo com a Lei de Snell para refração
Assim, o ângulo de polarização é dado por
Algo interessante que pode acontecer é que, caso a luz incidente seja polarizada paralela ao plano de incidência, ela não terá nenhuma componente perpendicular ao mesmo.
Mas no ângulo de Brewster, a luz refletida é perpendicular!
O que aconteceria então?
Nenhuma luz seria refletida. Na verdade, o que aconteceria é que a luz iria sumir!
Polarização por reflexão
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 35-69
Um raio de luz que está se propagando na água (índice de refração ) incide em uma placa de vidro cujo índice de refração é .
Para que ângulo de incidência a luz refletida é totalmente polarizada?
Passo 1
A luz refletida é totalmente polarizada quando ela incide em um material com o ângulo de Brewster.
Esse ângulo é tal que o raio refletido e o raio refratado têm um ângulo de entre si, fazendo com que os ângulos de refração e de reflexão somem e tenhamos:
Onde é o ângulo de incidência da luz, é o índice de refração do meio no qual a luz refrata (no caso, a placa de vidro com ) e é o índice de refração do meio no qual a luz se propagava (no caso, a água com ).
Substituindo:
Resposta
Exercício Resolvido #2
UFRJ, Física 4, Prova 1, 2015.1
O ângulo de incidência de um feixe de luz numa superfície refletora pode ser continuamente variado. Para certo material, o feixe refletido é completamente polarizado quando o ângulo de incidência é igual a .
O índice de refração deste material é igual a:
Nenhuma das anteriores
Passo 1
Na polarização por reflexão, quando a luz não-polarizada incide sobre a superfície que separa o ar do material, existe um ângulo específico no qual a luz refletida é completamente polarizada. Esse ângulo é chamado de ângulo de polarização.
Nesse caso, como a superfície separa o ar de um certo material, o ângulo de polarização é dado por:
Onde e são os índices de refração do material e do ar, respectivamente.
Logo, para :
Resposta
Exercício Resolvido #3
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 30-33.27
Um feixe paralelo de luz não-polarizada proveniente do ar incide formando um ângulo de (com a normal) sobre uma superfície plana de vidro.
O feixe refletido é completa e linearmente polarizado.
- Qual é o índice de refração do vidro?
- Qual é o ângulo de refração do feixe transmitido?
Passo 1
Trata-se de um problema de polarização por reflexão.
Sabemos então que a luz é completa e linearmente polarizada quando refletida somente se o ângulo de incidência for igual ao ângulo de polarização. Logo:
Sabemos que o ângulo de polarização estará relacionado com os índices de refração através da seguinte equação:
Sabemos também que os ângulos de polarização e de refração estão relacionados por
Passo 2
Letra a)
Onde:
;
;
;
Logo:
Passo 3
Letra b)
Sabemos que
Onde:
;
Logo:
Resposta
Letra a)
Letra b)
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 35-70
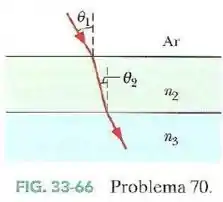
Na Fig.33-66 um raio luminoso que estava se propagando inicialmente no ar incide em um material com um índice de refração . Abaixo do material está o material , com um índice de refração .
O raio incide na interface ar-material com o ângulo de Brewster para essa interface e incide na interface material -material com o ângulo de Brewster para essa interface.
Qual é o valor de ?
Passo 1
Vamos passo a passo, para não nos perdermos.
O raio luminoso que incide no material incide com o ângulo de Brewster. Com isso, podemos dizer que:
Pois .
O enunciado nos diz que , e podemos achar o ângulo
Passo 2
Sabendo o ângulo , nós podemos achar pois quando o ângulo de incidência é o ângulo de Brewster a sua soma com o ângulo de refração é .
Passo 3
O enunciado nos diz que o ângulo de incidência na interface material -material é o ângulo de Brewster. Ou seja, é o ângulo de Brewster.
Passo 4
Vou mostrar um outro jeito de resolver o problema, que vai nos dar uma resposta exata, mas que talvez não seja tão óbvio de se imaginar. A idéia é fazer tudo de forma literal.
Sabemos que:
Além disso:
Substituindo:
Como dissemos, sendo o ângulo de Brewster, teremos:
Por fim, vamos ver uma identidade trigonométrica:
O que mostra que: