Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 78

Um raio de luz passa atraves de um prisma com um angulo de apice a,como mostrado na Figura 31-62.Oraio e a bissetriz. do angulo de apice se interceptam em angulos retos.Mostre que o angulo de desvio 8 esta relacionado ao ingulo de apice e ao indice de refracao do material do prisma por s e n ⁡ 1 2 ( α + δ ) = n s e n ⁡ 1 2 α

Passo 1

E aiiii gente, vem fazer essa questão tranquilíssima comigo!

Segura na minha mão, e vem!

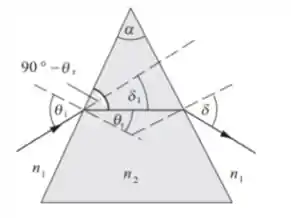
O diagrama à direita mostra os ângulos de incidência, refração e desvio na primeira interface. Podemos usar a geometria desta passagem simétrica da luz para expressar θ r em termos de α e δ 1 , em termos de θ r e α   . Podemos então usar um argumento de simetria para expressar o desvio na segunda interface e o total desvio δ . Finalmente, podemos aplicar a lei de Snell na primeira interface para completar a derivação da expressão dada.

Passo 2

Com relação à normal à face esquerda do prisma, deixe o ângulo de incidência ser θ i e o ângulo de refração ser θ r . A partir da geometria da figura, é evidente que:

θ r = 1 2 α

Expresse o ângulo de desvio na superfície de contato:

δ 1 = θ 1 - θ r = θ 1 - 1 2 α

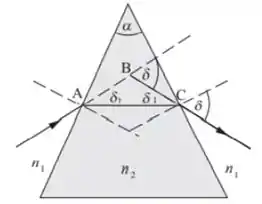
Referindo-se ao triângulo ABC, vemos que:

δ = 2 δ 1 = 2 θ 1 - 1 2 α = 2 θ 1 - α

Passo 3

Resolvendo para θ 1 , temos:

θ 1 = 1 2 ( α + δ )

Aplicar a lei de Snell, com n 1 = 1 e n 2 = n , para a primeira interface:

s i n ⁡ θ i = n s i n ⁡ 1 2 α

Substitua por θ 1 para obter:

sin ⁡ α + δ 2 = n sin ⁡ α 2                 ( 1 )

Resposta

V e r   r e s o l u ç ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um raio de luz solar não-polarizada atinge a parede plástica vertical de um tanque de água em um ângulo desconhecido. Parte da luz se reflete na parede e entra na água (Figura 33.60). O índice de refr
Certo cristal birrefringente possui índices de refração n 1 e n 2 para os dois componentes perpendiculares da luz linearmente polarizada que passa através do cristal. Os comprimentos de onda correspon
Um feixe de luz propagando-se horizontalmente apresenta um componente não-polarizado com intensidade I 0 e um componente polarizado com intensidade I p . O plano de polarização do componente polarizad
Considere duas vibrações com a mesma frequência e a mesma amplitude, porém com fases diferentes, uma ao longo do eixo Ox. x = a sen ⁡ ( ω t - α ) E aoutra ao longo do eixo Oy, y = a sen ⁡ ( ω t - β )
O ângulo de incidência θ 1 para o qual o raio refletido é perpendicular ao raio refratado chama-se ângulo de Brewster. (a) Obtenha o ângulo de Brewster θ 1 B em função do índice de refração relativo n