Múltiplas Refrações
Teoria
Às vezes os professores tentam colocar algumas questões em prova ou lista de exercício com as quais ele acha que vai conseguir pegar o aluno desprevenido.
São questões aparentemente super complicadas, mas que tem alguns macetes pra serem resolvidas.
Vou te falar um exemplo:
Um raio de luz se propaga no ar, e incide em uma placa de vidro, com índice de refração com um ângulo de incidência de .
A interface ar/vidro é plana e a luz que refrata no vidro depois incide em mais uma interface com um material novo com índice de refração . Essa nova interface é paralela à anterior.
A luz que refrata nesse material depois refrata em mais outro material, e depois mais outro, e mais outro e outro e outro, todos com as interfaces paralelas!
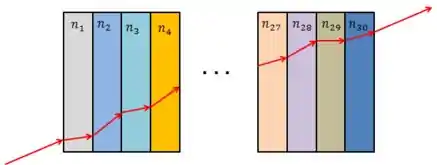
Isso se repete trinta vezes, até que a luz sai do último material de volta para o ar.
A pergunta é: Qual o ângulo que o raio luminoso que sai do sistema faz com a normal à superfície?
Quando temos interfaces paralelas, o ângulo de refração que a luz faz em um meio e o ângulo de incidência que ela faz no meio seguinte são iguais!
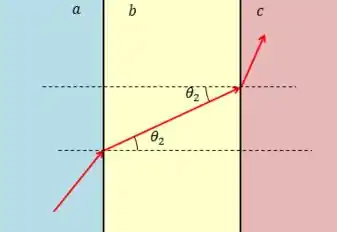
Pois sendo as interfaces paralelas, as retas normais a elas também serão.
Isso nos permite usar a Lei de Snell várias vezes com os mesmos ângulos de refração e incidência:
Onde é o ângulo de incidência do ar no meio e é o ângulo do raio luminoso que sai do conjunto devolta pro ar.
Como todos os termos são iguais, podemos simplesmente pegar o primeiro e o último:
Cortando os índices de refração um com o outro, e como os ângulos são menores que , podemos dizer que o ângulo de saída é igual ao ângulo de entrada do raio luminoso. E isso independe de quantos materiais colocamos no trajeto do raio!
Poderíamos usar o mesmo raciocínio pra achar o ângulo do raio em qualquer um dos materiais:
Pois é tudo igual mesmo.
E nem precisava ser ar no início. Podemos pegar dois termos no meio das igualdades.
Agora vamos pros exercícios, sem ser pego na pegadinha do malandro!
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 28-10
Na Fig.33-35 a luz começa no material , passa por placas feitas de três outros materiais com as interfaces todas paralelas entre si e penetra em outra placa do material .
A figura mostra o raio incidente e os raios refratados nas diferentes interfaces.
Coloque os materiais na ordem do índice de refração, começando pelo maior.
Passo 1
Quando um raio luminoso passa de um meio com índice de refração para um meio com índice de refração , temos:
Se, e somente se , o ângulo que o raio refratado faz com o vetor normal à interface dos meios é menor que o ângulo do raio incidente
Se, e somente se , o ângulo que o raio refratado faz com o vetor normal à interface dos meio é maior que o ângulo do raio incidente.
Logo, podemos comparar o índice de refração de duas placas em sequência pelo ângulo dos raios incidente e refratado.
Passo 2
Ao sair de e entrar em , o raio de luz faz um ângulo menor com a normal à superfície entre e . Por isso, .
De para o ângulo de refração é maior que o de incidência, e logo .
De para o ângulo decresce, o que significa que .
De para o ângulo cresce, indicando que
Passo 3
Agora temos um segundo problema:
Sabemos, por exemplo, que ambos e são maiores que e . Mas quem é maior entre e ?
A lei de Snell pode nos responder isso! Nesse caso, podemos aplica-la diversas vezes, o que nos dirá que:
Pois o âgulo de refração em será o mesmo que o incidente em e o de refração em será o mesmo que o de incidência em .
Isso nos diz que:
O que significa que, se o ângulo de refração em for maior que o em , , o e para os dois lados ficarem iguals, o índice de refração de precisaria ser menor que o de .
Porém o ângulo de refração em é menor que o de , o que nos diz que . Podemos fazer o mesmo para e :
E sendo o ângulo de refração em maior que o incidente entre e , isso significa que .
Por esse raciocínio, juntando todos os passos:
Resposta
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 36-76
Na Fig.33-72 dois raios luminosos que estavam se propagando inicialmente no ar passam por cinco placas de plástico transparente e voltam para o ar. As placas têm interfaces paralelas e espessura desconhecida; os índices de refração são , , , e .
O ângulo de incidência do raio é . Em relação à normal à última interface, determine:
- O ângulo de saída do raio .
- O ângulo de saída do raio .
- Do raio .
- Do raio .
(Sugestão: Pode ser mais rápido resolver o problema algebricamente.)
Se em vez de ar houver um vidro com um índice de refração à esquerda e à direita das placas, determine o ângulo de saída:
Passo 1
Letra a)
Quando o raio passa de um meio para outro perpendicular à interface, o raio propagado no segundo meio também vai ter uma direção normal à interface.
Por isso o raio vai atravessar todas as placas perpendicular às interfaces, e acabará saindo no fim com o mesmo ângulo no ar.
Logo, seu ângulo de saída é zero.
Passo 2
Letra b)
Como as interfaces de todas as placas são paralelas, podemos usar a lei de Snell consecutivas vezes usando o mesmo ângulo para dois usos em sequência.
Se usarmos apenas os dois extremos da equação:
Sendo os dois ângulos menores que , podemos dizer que
O ângulo de saída será igual ao de entrada .
Passo 3
Letra c)
Se invés de ar, tivéssemos vidro dos dois lados, nosso raciocínio para um raio perpendicular seria o mesmo.
Logo, o ângulo de saída do raio continuaria sendo zero.
Passo 4
Letra d)
Novamente, o raciocínio se mantém, e o ângulo de saída será igual ao de entrada.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 33-53
Na Fig.33-55 a luz incide, fazendo um ângulo com a normal, na interface de dois materiais transparentes. Parte da luz atravessa as outras três camadas transparentes e parte é refletida para cima e escapa para o ar.
Se , , , e , determine o valor:
- De
- De
Passo 1
Letra a)
Pela lei da reflexão, o raio refletido na interface de com terá o mesmo ângulo que o ângulo de incidência.
Como ele incide em uma interface paralela a essa entre e o ar, o ângulo de incidência nesse plano será o mesmo que o de reflexão.
Usando a lei de Snell:
Sabemos que , e pelo enunciado:
Passo 2
Letra b)
As interfaces são todas paralelas e nós podemos usar a lei de Snell para dizer:
Ou seja:
O índice de refração de é .
Resposta
Letra a)
Letra b)
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 34-59
Na Fig.33-59 um feixe luminoso que se propaga inicialmente no material é refratado para o material , atravessa esse material e incide com o ângulo crítico na interface dos meios e .
Os índices de refração são , e .
- Qual é o valor do ângulo ?
- Se o valor de aumenta, a luz consegue penetrar no meio ?
Passo 1
Letra a)
O raio que incide no material com um ângulo é refratado com um ângulo dado pela lei de Snell
Agora precisamos encontrar .
Passo 2
Podemos ver que temos um triângulo retângulo formado pelo raio refratado no meio e o ponto onde a luz incide nas interfaces entre e e entre e . Com isso, podemos encontrar o ângulo de incidência na interface entre e .
Usando a lei de Snell:
Mas pelo enunciado, é o ângulo crítico, o que significa que , e também:
A trigonometria também nos diz que .
Passo 3
Substituindo na nossa primeira equação junto com :
Passo 4
Letra b)
Se aumentar, aumenta e diminui, diminuindo o ângulo de refração e possibilitando que a luz penetre no meio .
Resposta
Letra a)
Letra b)
Sim, se o valor de aumenta a luz consegue penetrar no meio .
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 34-63
A Fig.33-62 mostra uma fibra ótica simplificada: um núcleo de plástico () envolvido por um revestimento de plástico com um índice de refração menor ().
Um raio luminoso incide em uma das extremidades da fibra com um ângulo . O raio deve sofrer reflexão interna total no ponto , onde atinge a interface núcleo-revestimento.
(Isso é necessário para que não haja perda de luz cada vez que o raio incide na interface.)
Qual é o maior valor de para o qual existe reflexão interna total no ponto ?
Passo 1
O ângulo de refração do feixe no núcleo de plástico da fibra ótica será:
Lembrando que o índice de refração do ar é :
Passo 2
Quando a luz que se propaga no núcleo de plástico e atinge a interface com o revestimento, ela sofre reflexão interna total.
O maior ângulo de incidência para o qual isso ocorre corresponde a um ângulo de refração de . Ou seja:
Substituindo os valores dados no enunciado:
Passo 3
Agora vamos conectar os dois passos dados.
Para isso, precisamos fazer uma construção geométrica. Vamos ver lateralmente o raio saindo do ar, incidindo no núcleo de plástico e depois no revestimento:
Podemos formar um triângulo retângulo entre o ponto que o raio de luz entra e o ponto que ele sofre reflexão total.
Por isso o ângulo de incidência vai ser . Rearrumando:
Substituindo na nossa primeira equação: