Reflexão Total
Produzido por Bruno SoaresTeoria
Na Reflexão Total a luz incidente é totalmente refletida. Esse fenômeno acontece quando incidimos uma luz de um meio mais refratante para um meio menos refratante em um ângulo maior que o ângulo limite. Assim:

📢 Clique para ver mais:
Lei de Snell
Quando a luz que se propaga em um meio
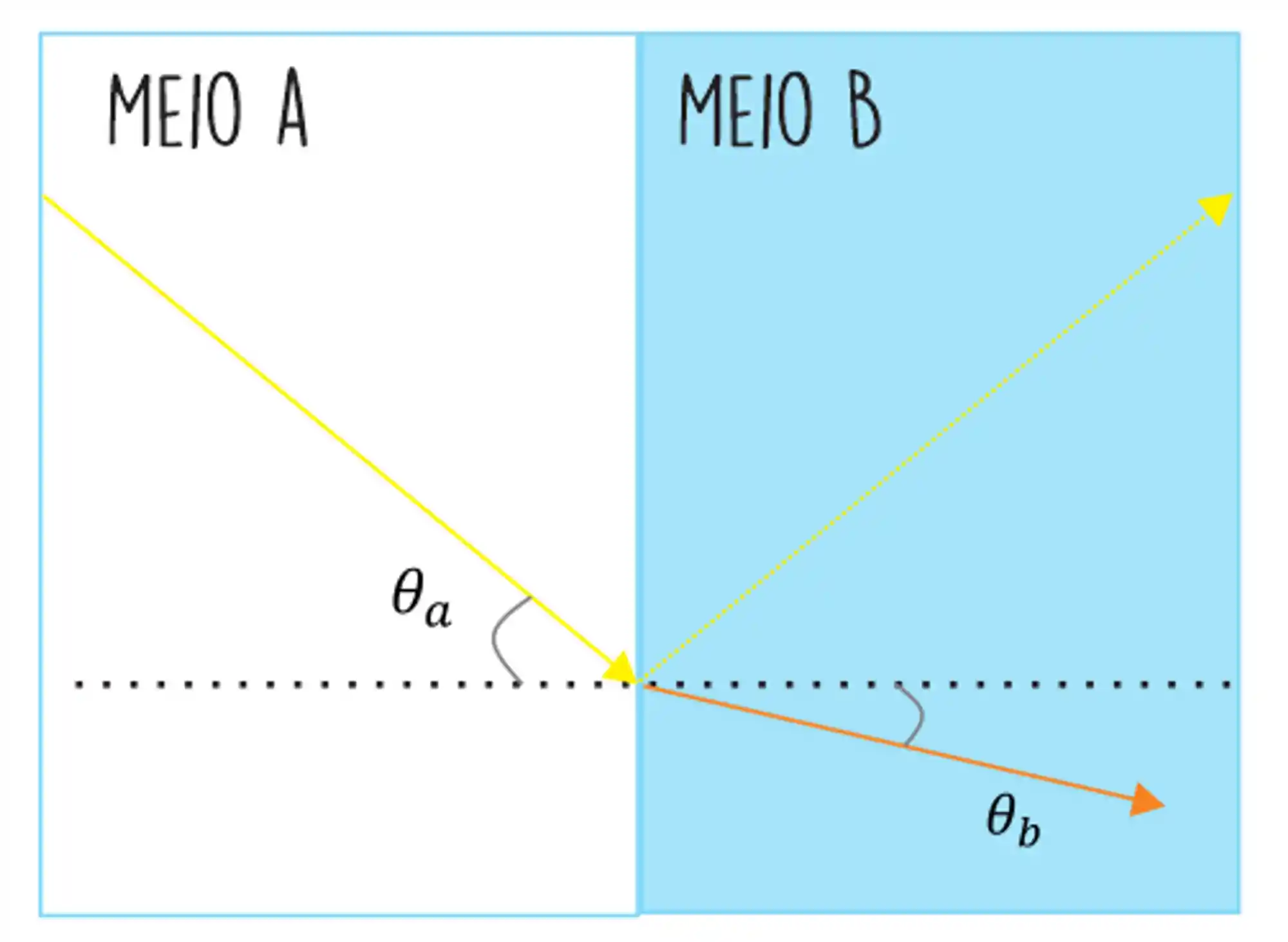
O ângulo de refração da luz pode ser dado pela lei de Snell:
Ela nos diz que, quando $n_b
Quer entender melhor como funciona o fenômeno de Reflexão Total? Então se liga nesse vídeo completaço que o Responde Aí preparou pra você? 👇👇👇
Reflexão Interna Total
Como vimos pela lei de Snell quando o índice de refração do meio
Nesse caso a Lei de Snell não vale mais! Se liga na imagem abaixo:
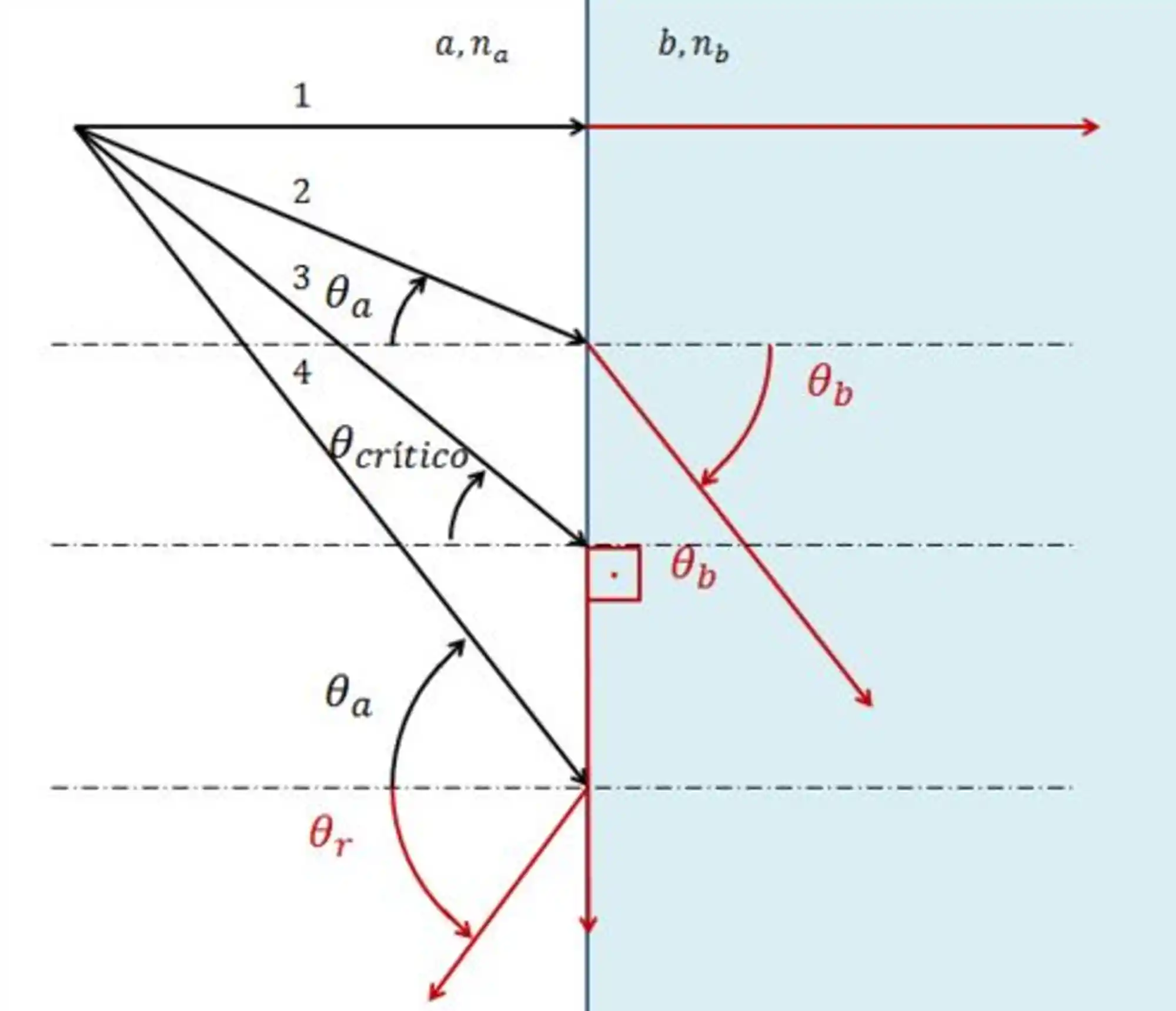
1 -Ângulos de Incidência e Refração Nulos
Inicialmente, os raios de incidência e refratado estão alinhados horizontalmente. Assim, os ângulos de incidência
2 -Ângulo de Refração maior que o Ângulo de Incidência
Agora, o ângulo
3 -Ângulo Limite
O ângulo de incidência aumenta até atingir o seu valor crítico. Neste ponto o ângulo de refração vale 90° e chamamos o ângulo de incidência de ângulo crítico
Podemos determinar o valor de
Onde
4 -Ângulo maior que 90º: Reflexão interna total
Se o ângulo
Um caso importante desse fenômeno é que caso você tente acender uma lâmpada dentro da água, a pessoa do lado de fora só conseguiria ver um círculo na superfície da água.
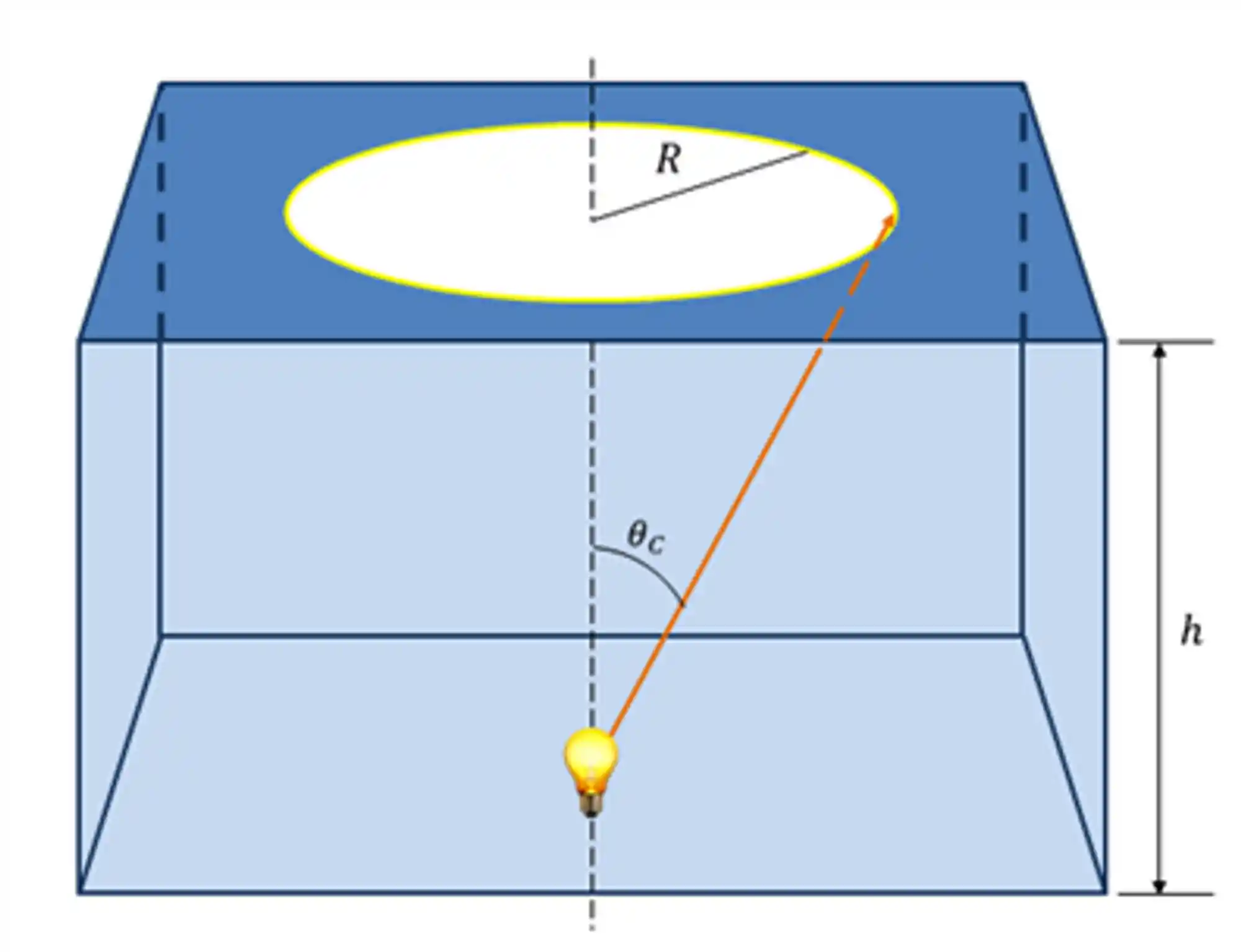
O índice de refração do ar é menor que o índice de refração da água e por isso a partir de um certo ângulo crítico toda a luz da lâmpada que sairia da água pro ar é refletida de volta. É possível calcular o raio desse círculo a partir do ângulo crítico:
Onde
Agora vamos praticar com exercícios?!
Reflexão Interna Total
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 34-58
O índice de refração do benzeno é .
Qual é o ângulo crítico para um raio luminoso que se propaga no benzeno em direção a uma interface plana do benzeno com o ar?
Passo 1
Quando um raio luminoso que se propaga no benzeno sofre refração numa interface plana com o ar, o ângulo de refração é maior que o ângulo de incidência pois .
Podemos dizer então que teremos um ângulo de incidência crítico tal que o ângulo de refração vai ser e para ângulos não há nenhum raio refratado.
Passo 2
Substituindo as condições acima na Lei de Snell:
Resposta
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 28-11
A Fig.33-36 mostra quatro placas horizontais , , e feitas de materiais diferentes, com ar acima da primeira placa e abaixo da última. O índice de refração dos materiais é dado.
Raios de luz incidem na extremidade esquerda das quatro placas, da forma indicada na figura.
Em que placa (identifique-a através do índice de refração) existe a possibilidade de que a luz fique confinada de tal forma que, após muitas reflexões, chegue à extremidade direita sem deixar a placa?

Passo 1
Para que um raio de luz, ao incidir na extremidade da placa, permaneça confinado na mesma, é necessário que haja um ângulo crítico entre os dois meios, ou seja, que o índice de refração do meio no qual a luz se propaga seja maior que o índice de refração do meio em cuja interface a luz incide.
Quando o ângulo de refração será maior que o ângulo de incidência, fazendo com que seja possível termos ângulos de incidência onde não há nenhuma refração (pois o ângulo seria maior que ).
Passo 2
Ao incidir na parte de cima da placa de forma que não seja refratado, o raio de luz é totalmente refletido de volta para a placa.
Neste caso, é possível que o raio incida novamente na parte de baixo da placa.
O raio se manterá confinado no meio no qual se propaga caso haja possibilidade de reflexão total nessa interface também, ou seja:
O que fará, novamente, o ângulo de refração ser maior que o ângulo de incidência.
Passo 3
Resumindo os passos anteriores, para que um raio possa se manter confinado numa placa ao entrar pelo lado esquerdo sofrendo múltiplas reflexões até sair pelo lado direito, precisamos ter:

A única placa que segue essa restrição é a placa com .
Resposta
Placa com .
Exercício Resolvido #3
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 30-33.21, modificado
Um raio de luz está se propagando em um cubo de vidro que está completamente imerso na água.
Você descobre que, se o raio incide sobre a interface vidro-água em um ângulo maior do que com a normal, nenhuma luz é refratada para dentro da água, cujo índice de refração vale .
Qual é o índice de refração do vidro?
Passo 1
O problema já nos diz os dois meios em que vamos trabalhar: água e vidro. De forma que o raio luminoso está se propagando inicialmente no cubo de vidro.
Através do enunciado, descobrimos que o ângulo crítico vale .
Sabemos que o ângulo crítico é calculado por:
Passo 2
Onde:
;
;
;
Logo:
Resposta
Exercício Resolvido #4
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 29-33.17, modificado
A luz entra em um tubo sólido feito de plástico e que possui um índice de refração igual a .
A luz desloca-se paralelamente à parte superior do tubo, conforme a figura abaixo.
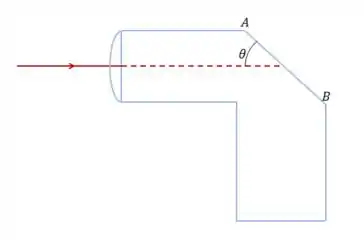
Você deseja cortar a face de modo que toda a luz seja refletida de volta para dentro do tubo depois de atingir essa face.
- Qual é o maior ângulo possível se o tubo está no ar?
- Se o tubo for imerso em água, cujo índice de refração é de , qual é o maior ângulo possível?
Passo 1
O problema nos dá o índice de refração do plástico .
O problema explica que o raio luminoso se propaga no plástico e incide sobre a superfície que separa o plástico do ar.
É importante chamar a atenção para o fato de que, quando o problema pede para calcularmos o maior ângulo possível , normalmente nós associamos ao ângulo crítico .
Porém, o ângulo pedido pelo problema não é o mesmo que o ângulo crítico .
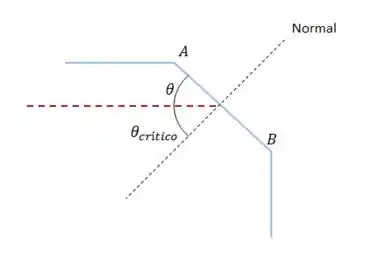
A figura acima é um zoom da região que estamos analisando.
Através da figura, vemos que, na verdade, os ângulos e estão relacionados por:
Passo 2
Letra a)
Tubo de plástico está no ar.
Podemos achar o ângulo crítico através da equação:
Onde:
;
;
Logo:
Assim:
Passo 3
Letra b)
Tubo imerso na água.
Os cálculos são os mesmos, portanto:
Onde:
;
;
Logo:
Assim:
Resposta
Letra a)
Letra b)
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 34-65, modificado
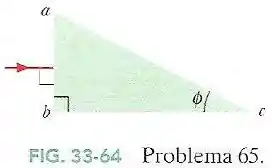
Na Fig.33-64 um raio luminoso incide perpendicularmente à face de um prisma de vidro ().
Determine o maior valor do ângulo para o qual um raio é totalmente refletido na face do prisma se este está imerso:
- No ar
- Na água (cujo índice de refração é )
Passo 1
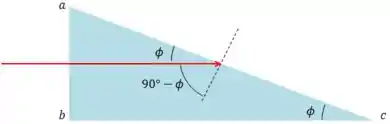
Antes de partimos para resolver cada item, vamos observar a geometria do problema.
O raio luminoso vai entrar no prisma paralelamente ao lado , pois ambos o raio e esse lado são perpendiculares ao lado .
Por serem paralelos, o ângulo que o raio faz com o lado vai ser o mesmo, .
Isso significa que o ângulo de incidência é .
Passo 2
Letra a)
Seja o ângulo de incidência. Ele vai ser o ângulo crítico quando o ângulo de refração . Substituindo na lei de Snell:
Pelo enunciado e temos que lembrar que .
Tem uma relação trigonométrica que diz que:
Logo:
Passo 3
Letra b)
Quando estamos na água, a única coisa que muda em relação ao ar é o índice de refração do meio externo ao prisma. Fazemos então os mesmos passos.
Resposta
Letra a)
Letra b)
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 34-60, modificado
Um peixe-gato está abaixo da superfície de um lago.
- Qual é o diâmetro da circunferência na superfície que delimita a região na qual o peixe pode ver o que existe do lado de fora do lago?
- Se o peixe desce para uma profundidade maior, o diâmetro da circunferência aumenta, diminui ou continua o mesmo?
Considere o índice de refração da água .
Passo 1
Letra a)
O diâmetro da circunferência na superfície pedida pode ser encontrada usando o ângulo crítico da refração da luz que sai da água.
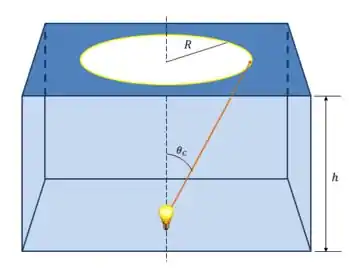
Para ângulos maiores que o crítico, a luz não sairá da água.
Pela geometria do problema, teremos:
Onde é o raio da circunferência e é a altura do peixe gato. Como o diâmetro é duas vezes o raio:
Passo 2
Agora precisamos achar o ângulo crítico.
Ele vai ser o ângulo tal que o ângulo de refração da luz no ar vai ser . Pela Lei de Snell:
Substituindo na fórmula do diâmetro, junto com a profundidade do peixe gato:
Passo 3
Letra b)
O diâmetro da circunferência é diretamente proporcional à profundidade do peixe gato.
Isso significa que quanto maior a profundidade, maior o diâmetro.
Logo, se o peixe gato descer para uma profundidade maior, o diâmetro vai aumentar.
Resposta
Letra a)
Letra b)
Se o peixe gato descer para uma profundidade maior o diâmetro vai aumentar.