Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 14.Exercícios e Problemas - Ex. 10
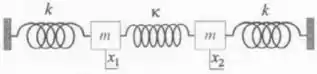
. Os deslocamentos dos blocos vistos na Figura em relação ao equilíbrio são e . Mostre que a energia potencial do sistema pode ser escrita na forma . Escreva a Lagrangeana do sistema. Escreva as equações de Lagrange do sistema. Supondo que o movimento do sistema seja da forma , calcule as suas frequências naturais.
Passo 1
Vem comigo que a gente detona a questão!
A energia potencial desse sistema é dada apenas pelas energias potências elásticas de cada mola. A energia potencial elástica é dada por:
Onde é o quanto a mola se deslocou da posição de equilíbrio. Então vamos avaliar essa condição para cada mola e montar a energia potencial de cada uma e depois do sistema.
Para escrever a Lagrangeana temos que lembrar que:
A energia potencial já teremos do item , então só teremos que a achar a energia cinética, de cada bloco.
Teremos que escrever a equação de Lagrange para as coordenadas generalizadas e , a equações são da seguinte forma:
Depois vamos analisar essas equações para encontrarmos as frequências naturais e .
Passo 2
Vamos montar a energia potencial.
Para a primeira mola (da esquerda para a direita), temos:
Já que como é o deslocamento do bloco em relação a posição de equilíbrio da mola, então acaba sendo a deformação da mola.
A mesma coisa ocorre para a terceira mola, assim:
Agora para a segunda mola, temos que notar que ela sofre deformação por meio dos seus dois extremos, por um lado ela sofre uma deformação e pelo outro ela sofre uma deformação de , então sua deformação total é:
Assim sua energia potencial elástica é dada por:
A energia potencial do sistema é dada por:
Passo 3
Agora vamos ver a energia cinética do sistema. Essa energia vai ser dada pela soma das energias cinéticas de cada bloco, assim:
Usando que:
Assim temos:
Com isso, a nossa Lagrangeana fica da seguinte forma:
Passo 4
Agora vamos escrever a equação de Lagrange para . Vamos calcular cada parte da equação separadamente depois juntamos tudo.
Primeiro vamos calcular , temos:
Agora vamos calcular , então:
Agora por último , temos:
Juntando tudo temos:
Passo 5
Agora vamos escrever a equação de Lagrange para . Vamos calcular da mesma forma que fizemos no passo anterior.
Primeiro vamos calcular , temos:
Agora vamos calcular , então:
Agora por último , temos:
Juntando tudo temos:
Passo 6
Agora temos que achar as frequências naturais, para isso vamos fazer o seguinte, vamos isolar na última equação que obtemos, então:
Substituindo isso na primeira equação que encontramos, temos:
Para resolver isso vamos usar o método do polinômio característico, então:
Chamando:
Temos:
Fazendo , temos:
Que é uma equação de segundo grau.
Passo 7
Resolvendo a equação de segundo grau, temos:
Vamos substituir o que temos para e em cada raiz.
Primeiro:
Com isso temos que:
Segundo, temos:
Com isso temos que:
Agora, sabendo que:
Assim temos:
Do método dos polinômios característicos sabemos que o termo que multiplica nessas raízes são os argumentos dos cossenos da solução da equação e esse argumento é e , que são as frequências naturais, logo:
Resposta
Demonstrado acima