Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 116

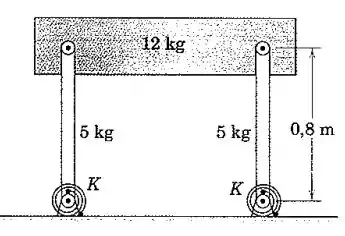
O bloco de 12 kg é apoiado pelas duas barras de 5kg com duas molas de torção, cada uma de constante K = 500 Nm/rad, dispostas como apresentado. As molas são suficientemente rígidas de modo que o equilíbrio estável é verificado na posição mostrada. Determine a frequência natural para pequenas oscilações em torno dessa posição de equilíbrio.

Passo 1

Bom pessoal, como as barras possuem o mesmo tamanho, estão na vertical e possuem a mesma mola de apoio, então o bloco não possui rotação, apenas translação. Já as barras possuem apenas rotação. Podemos então escrever a equação da energia cinética da seguinte forma:

Um detalhe importante: As barras giram em torno das molas, e não em torno do seu centro de massa. Então, o momento de inércia pode ser obtido pelo teorema dos eixos paralelos:

Substituindo na equação:

Passo 2

Agora vamos para a parte de energia potencial.

A energia potencial do sistema é igual soma das variações da energia potencial elástica e da gravitacional.

Vamos primeiro analisar a energia potencial gravitacional, com a ajuda da figura abaixo, representando uma das barras:

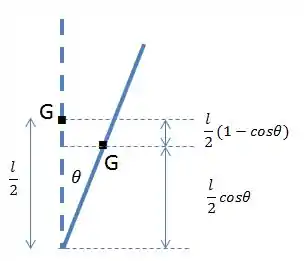
Quando a barra se desloca um ângulo para a direita, o centro de massa da massa desce . Por estar localizado no final da barra, por proporção, o bloco vai descer duas vezes esta altura . Importante não esquecer que como as massas estão perdendo altura, sua energia é negativa.

Bom, já a energia potencial elástica é simplesmente dada pelo deslocamento , lembrando sempre que são 2 barras.

Podemos então escrever a equação da energia potencial:

Agora, vamos voltar para a equação de energia do sistema. Basta juntar as equações (1) e (2):

Como o sistema é conservativo, (Não esquecer a regra da cadeira):

Para pequenos ângulos, usamos a aproximação

Ajeitando a equação:

Substituindo os valores, temos que:

Agora temos uma equação nos moldes da equação do movimento harmônico. Com isto, sabemos a frequência natural:

Podemos relacionar a frequência à velocidade angular:

Substituindo na equação, temos que:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9 . (Repetição de problema do Capítulo 13 , Oscilador harmônico.) Ao oscilar forçado pela mola, o cilindro visto na figura 14.9 rola sobre o piso, girando livremente em torno do seu eixo. A ) Escreva

11 . A Figura 14.11 mostra uma esfera de raio r e massa m que rola dentro de um parabolóide. Um corte no plano x y do parabolóide gera uma parábola cuja equação é y = 1 2 C x 2 . A ) Escreva a lagrang

8 . A barra fina vista na Figura 14.8 , cm comprimento l e massa m , oscila como um pêndulo em torno de um eixo à distância b da sua extremidade superior. A ) Escreva a lagrangeana do pêndulo. B ) Cal

10 . Os deslocamentos dos blocos vistos na Figura ( 14.10 ) em relação ao equilíbrio são x 1 e x 2 . A ) Mostre que a energia potencial do sistema pode ser escrita na forma V = 1 2 k x 1 2 + x 2 2 + 1

Quando o deslocamento em um MHS é metade da amplitude x m , que fração da energia total é (a) energia cinética e (b) energia potencial? (c) Para que deslocamento, como fração da amplitude, a energia d