Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 114
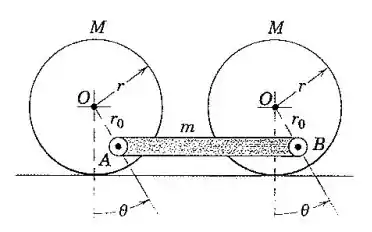
Desenvolva a expressão para a frequência natural do sistema composto de dois cilindros circulares homogêneos, cada um de massa M, e o elemento de ligação AB de massa m. Assuma pequenas oscilações.
Passo 1
Bom pessoal, vamos primeiro discutir quais as componentes de energia atuam neste sistema.
Podemos observar que a barra AB não gira, apenas translada. Já as rodas transladam e giram. Então, a energia cinética do sistema pode ser escrita da forma:
O momento de inércia de uma roda é calculado da forma .
Já a velocidade do centro das rodas O pode ser calculada a partir do centro instantâneo, que é o ponto de contato com o solo. Temos então:
Agora vamos para a velocidade da barra AB. Bom, a velocidade da barra é a mesma por toda sua extensão, então podemos calcular a velocidade a partir do ponto A. Vejamos:
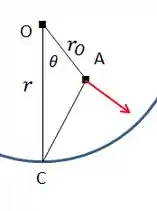
O módulo da velocidade de A pode ser calculado a partir do centro instantâneo como:
A distância entre A e C pode ser obtida pela lei dos cossenos no triângulo AOC:
Como na equação da energia, a velocidade está ao quadrado, vamos escrever logo dessa forma:
Agora, voltamos à equação da energia cinética e substituímos os valores:
Passo 2
Agora vamos para a parte de energia potencial.
As rodas permanecem com seus centros de massa na mesma altura, portanto não possuem variação na energia potencial gravitacional. Já a barra sobre uma variação de altura. Veja a figura abaixo, que compara quando A está no ponto mais baixo e quando ela anda um ângulo :
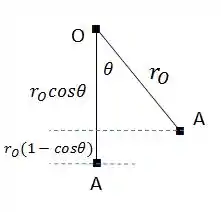
Lembrando que a barra está na horizontal, e, portanto o centro de massa da barra vai variar uma mesma altura que o ponto A. A energia potencial do sistema pode ser escrita como:
Agora, vamos para a equação de energia total. Basta juntar as equações (1) e (2):
Como o sistema é conservativo, (Não esquecer a regra da cadeira):
Agora vamos usar algumas aproximações. Como o ângulo é muito pequeno, o termo com maior expoente pode ser desprezado, ou seja, o termo . Além disso, o seno pode ser aproximado ao próprio ângulo , e o
Arrumando a equação para o termo a segunda ficar com o coeficiente unitário, temos:
Agora temos uma equação nos moldes da equação do movimento harmônico. Com isto, sabemos a frequência natural:
Podemos relacionar a frequência à velocidade angular:
Substituindo na equação, temos que: