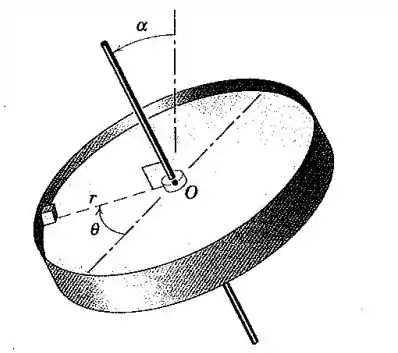
O eixo de rotação da plataforma giratória está inclinado em um ângulo a partir da vertical. A haste da plataforma é livremente articulada nos mancais que não são mostrados. Se um pequeno bloco de massa m é colocado a uma distancia a partir do ponto O, determine a frequência natural para pequenas oscilações rotacionais através do ângulo O momento de inércia de massa da plataforma giratória em relação ao eixo de sua haste é I.

Bom pessoal, nessa questão o que é mais complicado é enxergar o que está acontecendo e associar isso ao método de energia. Vamos então por partes:

Como sabemos, em um movimento harmônico simples, a energia é um balanço entre a energia cinética e a energia potencial, como mostra a equação:

Como o sistema é conservativo, a energia total E é uma constante. Além disso, nós temos que quando a energia cinética é máxima, a energia potencial é nula, e vice versa. Veja só:

Consideramos que a energia cinética é máxima no instante inicial do sistema, isto é, Então, quando:

Agora, vamos voltar para a equação do movimento harmônico e escrever de uma maneira mais completa de acordo com a questão.

Onde a energia cinética é composta pela energia cinética rotacional e pela energia cinética de translação .

A energia potencial neste caso é apenas gravitacional e pode ser escrita por:

Bom, o aparece pelo fato de a massa está “subindo”, o que faz aumentar sua energia potencial. Além disso, vemos que para , o que atende o que foi considerado acima. A parte do é pelo fato da componente da altura deslocada. Veja o diagrama.

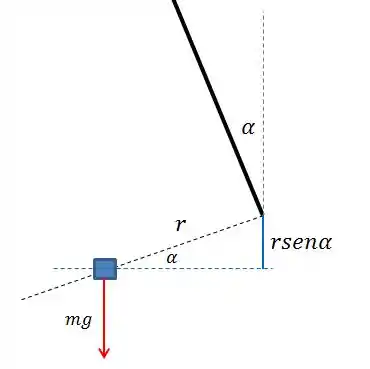
Beleza!! Agora vamos substituir os valores:

Como

Para ângulos muito pequenos, vale a aproximação:

Portanto:

Arrumando a equação para o termo a segunda ficar com o coeficiente unitário, temos:

Agora temos uma equação nos moldes da equação do movimento harmônico. Com isto, sabemos a frequência natural: