Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 30.6 - Ex. 54
54 Na , . Determine os valores de
- e
logo após o fechamento da chave S. (Considere positivas as correntes nos sentidos indicados na figura e negativas as correntes no sentido oposto.)
Determine também os valores de
e
muito tempo após o fechamento da chave.
A chave é aberta depois de ter permanecido fechada por muito tempo. Determine os valores de
e
logo depois de a chave ter sido novamente aberta.
Determine também os valores de
e
muito tempo depois de a chave ter sido novamente aberta.
Passo 1
Vamos analisar a tensão em cima do indutor:
E quando a chave é fechada o indutor está descarregado, portanto nenhuma corrente passa pelo indutor (agindo como uma chave aberta) reduzindo nosso circuito da seguinte forma:
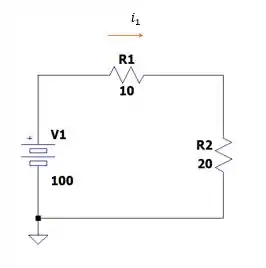
Ou seja:
E as correntes podem ser calculadas da seguinte forma:
Passo 2
Quando fechado por muito tempo o indutor ele passa a drenar o máximo de corrente ao ponto de a corrente sobre ela não variar mais, então a tensão nos terminais é nula (como passa corrente e não há tensão entre seus terminais considera-se uma chave fechada ) de modo a termos o seguinte circuito:
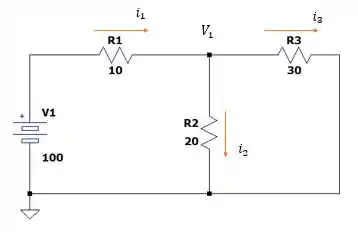
Fazendo a diferença de tensão em todos os nós do circuito nós temos:
Onde a somatória das correntes no nó de tensão igual a nos dá:
Igualando as equações e temos:
Aplicando esse resultado em :
Então a equação pode ser escrita como:
Então:
Por curiosidade a corrente no indutor será de:
Passo 3
Quando abrimos a chave depois de ter ficado muito tempo aberta (a situação do passo 2) toda a corrente que passa pelo resistor é jogada para terra, deixando de existir no mesmo instante, portanto:
Porém a corrente no em é proveniente do indutor que existe nesse circuito e inicialmente o indutor demora um tempo para notar que houve um cessamento de corrente, então ele ainda continua recebendo a corrente , de forma que temos o circuito abaixo.
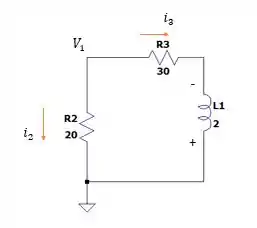
Então a corrente que passa no resistor será no mesmo sentido de de forma a tentar manter o que tinha antes (comportamento de oposição a mudança típico do indutor, por isso o pólo positivo do indutor fica virado pro terra pois a tendência é que diminua com o tempo e o indutor quer mais corrente e com isso o caminho mais rápido pro descarregamento magnético do indutor é pelo polo positivo que se forma nele).
Passo 4
Após muito tempo com a chave aberta toda a corrente que passa no circuito irá cessar, fazendo com que: