Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.Problemas Adicionais - Ex. 86

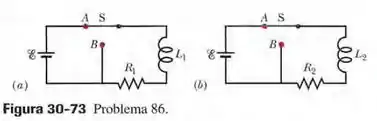
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00   m H e o resistor de resistência R 1 = 25,0   Ω se estabilizasse. Da mesma forma, na figura 30-73b, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 2 = 3,00   m H e o resistor de resistência R 2 = 30,0   Ω se estabilizasse. A razão ϕ 02 / ϕ 01 entre o fluzo magnético através de uma das espiras do indutor 1 é 1,50 . No instante t = 0 , as duas chaves são deslocadas para a posição B . Em que instante de tempo os fluxos magnéticos através de uma espira dos dois indutores são iguais?

Passo 1

Por conta do decaimento da corrente que acontece quando as chaves são deslocadas para a posição B , o fluxo magnético nos circuitos das figuras 30-73a e 30-73b decai de acordo com as equações

ϕ 1 = ϕ 10 e - t τ 1   e   ϕ 2 = ϕ 20 e - t τ 2

na qual as constantes de tempo são dadas por τ = L / R . Igualando os fluxo e explicitando o tempo, obtemos:

ϕ 10 e - t τ 1   = ϕ 20 e - t τ 2

ϕ 10 e R 1 t L 1 = ϕ 20 e R 2 t L 2

ϕ 20 ϕ 10 = e R 2 t L 2 e R 1 t L 1

ϕ 20 ϕ 10 = e R 2 t L 2 - R 1 t L 1

Passo 2

Vamos aplicar o logritmo natural nos dois membros da expressão:

ln ⁡ ϕ 20 ϕ 10 = ln ⁡ e R 2 t L 2 - R 1 t L 1

R 2 t L 2 - R 1 t L 1 = ln ⁡ ϕ 20 ϕ 10

t R 2 L 2 - R 1 L 1 = ln ⁡ ϕ 20 ϕ 10

t = ln ⁡ ϕ 20 ϕ 10 R 2 L 2 - R 1 L 1

Passo 3

Vamos agora aplicar os valores na expressão para encontrar o valor de t!

t = ln ⁡ ϕ 20 ϕ 10 R 2 L 2 - R 1 L 1 = ln ⁡ 1,50 30,0   Ω 0,0030   H - 25 , 0   Ω 0,00 5 0   H

t = 81,1   μ s

Resposta

O instante de tempo é igual a:

t = 81,1   μ s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a fem da bateria nu circuito da Fig. 33-6 varie com o tempo t de tal modo que a corrente seja dada por i ( t )=3,0+5,0 t , onde i é dado em amperes e t em segundos. Faça R=4,0 Ω ,L = 6.0H
Na Figura 33-17, E=100V ,R 1=10Ω ,R 2=20Ω ,R 3=30ΩeL=2H . Determine os valores de i 1ei 2 (a) imediatamente após o fechamento da chave S; (b) muito tempo depois do fechamento de S; (c) imediatamente a
No instante t =0 , ligamos uma bateria em série com um indutor e um resistor. A tabela abaixo dá a diferença de potencial, em volts, através do indutor após a ligação da bateria. Determinar (a) a fem
A energia armazenada num certo indutor e 25 mJ quando a corrente e 60 mA. (a) Calcular a indutância. (b) Que corrente e necessária para a energia magnética armazenada ser quatro vezes maior?
Uma diferença de potencial de 45,0 V é subitamente aplicada a uma bobina com L =50.0m HeR =180Ω . Qual é a taxa de crescimento da corrente após 1,20 ms?