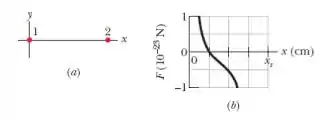
Na Fig. 21-27a, a partícula 1 (de carga ) e a partícula 2 (de carga ) são mantidas fixas no eixo , separadas por uma distância de . A força que as partículas 1 e 2 exercem sobre uma partícula 3 (de carga ) colocada entre elas é . A Fig. 21-27b mostra o valor da componente dessa força em função da coordenada do ponto em que a partícula 3 é colocada. A escala do eixo é definida por . Determine (a) o sinal da carga e (b) o valor da razão .
Passo 1
O problema informou que duas cargas e são posicionadas no eixo e separada por uma distância . Entre elas é colocada uma carga e a força resultante que atua sobre essa carga é dada na figura 21-27b.
No item (a) queremos saber o sinal da carga . Para isso, temos que olhar o que acontece com a força sobre quando ela é posicionada próxima de . Fazemos isso pois se ela estiver muito próxima da carga , a interação com a carga será bem menor (força cai com inverso do quadrado da distância), de modo que a maior controbuição para a força resultante será devido à interação com .
Com isso, olhamos no gráfico da força e vemos que para muito próximo de , a força resultante é positiva. Isso significa que a força que faz em aponta na direção positiva do eixo . Isso significa que a força entre essas duas cargas é repulsiva, de modo que elas devem ter o mesmo sinal. Como , achamos
Fazendo uma análise parecida com a carga próxima de , vemos que a força é negativa de modo que a interação entre e também é repulsiva e .
Passo 2
Vamos agora ao item (b). Queremos achar a razão
Como e , temos que
Vamos considerar a carga posicionada a uma distância da carga e da carga :
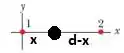
A força que aplica em é positiva e a força que aplica em é negativa, todas na direção . Lembre-se que as duas forças são repulsivas. Com isso, podemos escrever que a força resultante sobre é
Olhando para o gráfico da força, vemos que para
a força é nula. Isso significa que para esse valor de :
Assim, como e :
Portanto,