Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.Problemas Adicionais - Ex. 87
A chave da figura 30-61 é fechado no instante , fazendo com que a corrente comece a aumentar no indutor de e no resistor de . Em que instante a força eletromotriz entre os terminais do indutor é igual à diferença de potencial entre os terminais do resistor?
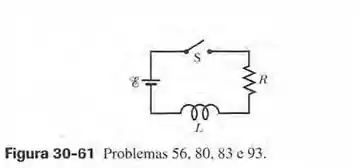
Passo 1
Estamos interessados nessa questão em determinar o instante no qual Como, de acordo com a lei das malhas, , isso significa que, nesse instante, .
A variação com o tempo da corrente no circuito é dado por:
Assim, podemos escrever :
Passo 2
Vamos aplicar o logaritmo natural em ambos os lados da expressão:
Passo 3
Vamos aplicar os valores que foram fornecidos no enunciado para encontrarmos o tempo.
Resposta
O instante é igual a:
Exercícios de Livros Relacionados
No circuito mostrado na Figura 28-54, seja ε 0 = 12,0V , R = 3,00Ω e L = 0,600H . A chave é fechada no instante t = 0 . Durante o tempo desde t = 0 até t = L / R , determine:a) A quantidade de energia
Tome como referência o Exercício 30.23. (a) Qual é a taxa com que a bateria está fornecendo energia elétrica ao circuito logo após ele estar fechado? (b) Quando a corrente tiver alcançado seu valor co
Na Figura 30.11, S 1 é fechada enquanto S 2 é mantida aberta. A indutância é L = 0,380H , a resistência é R = 48,0Ω , e a fem da bateria é 18,0V . No momento t após S 1 ser fechada, acorrente no circu
Na Figura 30.11, R =15,0Ω e a fem da bateria é igual a 6,30V . Com a chave S 2 aberta, S 1 é fechada. Depois de vários minutos, S 1 é aberta e S 2 é fechada. (a) 2,00m s após S 1 ser aberta, a corrent
48 . Considere o circuito na Figura 30.11 , com as duas chaves abertas. Em t = 0 , a chave S 1 é fechada enquanto S 2 é mantida aberta. ( a ) Use a Equação 30.14 para derivar uma equaçãopara a taxa P