Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.Problemas Adicionais - Ex. 85
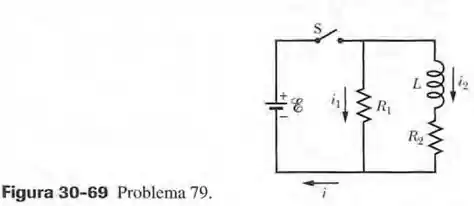
Na figura 30-69, a fonte é idela, , , e . A chave é fechada no instante . Determine logo depois do fechamento da chave (a) ; (b) ; (c) a corrente na chave; (d) a diferença de potencial entre os terminais do resistor 2; (e) a diferença de potencial entre os terminais do indutor; (f) a taxa de variação . Determine também, muito tempo após o fechamento da chave, (g) ; (h) ; (i) ; (j) ; (k) ; (l) .
Passo 1
Pessoal, essa questão é boa! É uma típica questão de circuitos RL. Vamos para a letra (a), que nos pede a corrente logo após o fechamento da chave. Nesse caso, como o resistor está em paralelo com a fonte de tensão, ambos tem a mesma tensão! Assim,
Passo 2
Na letra (b) queremos saber a corrente que passa pelo indutor e o segundo resistor. No entando, a corrente não pode variar bruscamente em um indutor, o que nos leva a ter:
Passo 3
Na letra (c) queremos achar a corrente que passa pela chave , . Num circuinto paralelo sabemos que as correntes que circulam nos ramos paralelos compõem a corrente que chega no nó em que elas se dividem, ou seja, a corrente que passa pela chave é igual a soma das correntes que seguem pelos ramos do circuito
Passo 4
Na letra (d) queremos achar a diferença de potencial nos terminais do resistor 2. Conforme resultado da letra (b), não temos corrente circulando por aquele ramo, inicialmente. Logo, a tensão será:
Passo 5
Na letra (e) queremos saber a tensão em cima do indutor. Nesse caso, a tensão sera igual a:
Passo 6
Na letra (f) queremos saber a variação da corrente . Assim,
Passo 7
Na letra (g), queremos saber a corrente que circula no primeiro ramo do circuito, a , depois de muito tempo após o fechamento da chave. Como não temos nenhum elemento que mude de características conforme o passar do tempo, continuamos tendo o mesmo resultado da letra (a):
Passo 8
Na letra (h), queremos a corrente no segundo ramo do circuito. Como depois de muito tempo a tensão em cima do indutor é zero, só resta o resistor. Assim,
Passo 9
Na letra (i), queremos a corrente que circula na chave . A corrente que passa em é a soma das correntes que circulam pelos ramos. Assim,
Passo 10
Na letra (j), queremos saber a tensão no resistor 2. Como
Passo 11
Na letra (k), queremos saber a tensão nos terminais do indutor. Como depois de muito tempo a tensão no indutor vai pra zero,
Passo 12
Por fim, na letra (l) queremos saber a variação da corrente no segundo ramo. Assim,
Resposta
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .